Why does $1+2+3+\cdots = -\frac{1}{12}$?

Question

$\displaystyle\sum_{n=1}^\infty \frac{1}{n^s}$ only converges to $\zeta(s)$ if $\text{Re}(s) > 1$.

Why should analytically continuing to $\zeta(-1)$ give the right answer?

Answer 1

there are many ways to see that your result is the right one. What does the right one mean?

It means that whenever such a sum appears anywhere in physics - I explicitly emphasize that not just in string theory, also in experimentally doable measurements of the Casimir force (between parallel metals resulting from quantized standing electromagnetic waves in between) - and one knows that the result is finite, the only possible finite part of the result that may be consistent with other symmetries of the problem (and that is actually confirmed experimentally whenever it is possible) is equal to $-1/12$.

It's another widespread misconception (see all the incorrect comments right below your question) that the zeta-function regularization is the only way how to calculate the proper value. Let me show a completely different calculation - one that is a homework exercise in Joe Polchinski's "String Theory" textbook.

Exponential regulator method

Add an exponentially decreasing regulator to make the sum convergent - so that the sum becomes $$ S = \sum_{n=1}^{\infty} n e^{-\epsilon n} $$ Note that this is not equivalent to generalizing the sum to the zeta-function. In the zeta-function, the $n$ is the base that is exponentiated to the $s$th power. Here, the regulator has $n$ in the exponent. Obviously, the original sum of natural numbers is obtained in the $\epsilon\to 0$ limit of the formula for $S$. In physics, $\epsilon$ would be viewed as a kind of "minimum distance" that can be resolved.

The sum above may be exactly evaluated and the result is (use Mathematica if you don't want to do it yourself, but you can do it yourself) $$ S = \frac{e^\epsilon}{(e^\epsilon-1)^2} $$ We will only need some Laurent expansion around $\epsilon = 0$. $$ S = \frac{1+\epsilon+\epsilon^2/2 + O(\epsilon^3)}{(\epsilon+\epsilon^2/2+\epsilon^3/6+O(\epsilon^4))^2} $$ We have $$ S = \frac{1}{\epsilon^2} \frac{1+\epsilon+\epsilon^2/2+O(\epsilon^3)}{(1+\epsilon/2+\epsilon^2/6+O(\epsilon^3))^2} $$ You see that the $1/\epsilon^2$ leading divergence survives and the next subleading term cancels. The resulting expansion may be calculated with this Mathematica command
1/epsilon^2 * Series[epsilon^2 Sum[n Exp[-n epsilon], {n, 1, Infinity}], {epsilon, 0, 5}]

and the result is $$ \frac{1}{\epsilon^2} - \frac{1}{12} + \frac{\epsilon^2}{240} + O(\epsilon^4) $$ In the $\epsilon\to 0$ limit we were interested in, the $\epsilon^2/240$ term as well as the smaller ones go to zero and may be erased. The leading divergence $1/\epsilon^2$ may be and must be canceled by a local counterterm - a vacuum energy term. This is true for the Casimir effect in electromagnetism (in this case, the cancelled pole may be interpreted as the sum of the zero-point energies in the case that no metals were bounding the region), zero-point energies in string theory, and everywhere else. The cancellation of the leading divergence is needed for physics to be finite - but one may guarantee that the counterterm won't affect the finite term, $-1/12$, which is the correct result of the sum.

In physics applications, $\epsilon$ would be dimensionful and its different powers are sharply separated and may be treated individually. That's why the local counterterms may eliminate the leading divergence but don't affect the finite part. That's also why you couldn't have used a more complex regulator, like $\exp(-(\epsilon+\epsilon^2)n)$.

There are many other, apparently inequivalent ways to compute the right value of the sum. It is not just the zeta function.

Euler's method

Let me present one more, slightly less modern, method that was used by Leonhard Euler to calculate that the sum of natural numbers is $-1/12$. It's of course a bit more heuristic but his heuristic approach showed that he had a good intuition and the derivation could be turned into a modern physics derivation, too.

We will work with two sums, $$ S = 1+2+3+4+5+\dots, \quad T = 1-2+3-4+5-\dots $$ Extrapolating the geometric and similar sums to the divergent (and, in this case, marginally divergent) domain of values of $x$, the expression $T$ may be summed according to the Taylor expansion $$ \frac{1}{(1+x)^2} = 1 - 2x + 3x^2 -4x^3 + \dots $$ Substitute $x=1$ to see that $T=+1/4$. The value of $S$ is easily calculated now: $$ T = (1+2+3+\dots) - 2\times (2+4+6+\dots) = (1+2+3+\dots) (1 - 4) = -3S$$ so $S=-T/3=-1/12$.

A zeta-function calculation

A somewhat unusual calculation of $\zeta(-1)=-1/12$ of mine may be found in the Pictures of Yellows Roses, a Czech student journal. The website no longer works, although a working snapshot of the original website is still available through the WebArchive (see this link). A 2014 English text with the same evaluation at the end can be found at The Reference Frame.

The comments were in Czech but the equations represent bulk of the language that really matters, so the Czech comments shouldn't be a problem. A new argument (subscript) $s$ is added to the zeta function. The new function is the old zeta function for $s=0$ and for $s=1$, it only differs by one. We Taylor expand around $s=0$ to get to $s=1$ and we find out that only a finite number of terms survives if the main argument $x$ is a non-positive integer. The resulting recursive relations for the zeta function allow us to compute the values of the zeta-function at integers smaller than $1$, and prove that the function vanishes at negative even values of $x$.

Answer 2

Here is a variant on Lubos Motl's answer:

Let $S = \sum_{n=1}^{\infty} n$. Then $S - 4 S = \sum_{n = 1}^{\infty} (-1)^{n-1} n.$ We will evaluate this latter expression with a regularization similar to Lubos Motl's.

Namely, consider $$\sum_{n=1}^{\infty} (-1)^{n-1} n t^n = -t \dfrac{d}{dt} \sum_{n=1}^{\infty} (-t)^n = -t \dfrac{d}{dt} \dfrac{1}{1+t} = \dfrac{t}{(1+t)^2}.$$
Letting $t \to 1,$ we find that $-3 S = \dfrac{1}{4}$, and hence that $S = \dfrac{-1}{12}.$

---

To see the relationship between this approach and Lubos Motl's, note that if we write $t = e^{\epsilon},$ then $t\dfrac{d}{dt} = \dfrac{d}{d\epsilon},$ so in fact the arguments are essentially the same, except that Lubos doesn't perform the initial step of replacing $S$ by $S - 4S$, which means that he has the pole $\dfrac{1}{\epsilon^2}$ which he then subtracts away.

---

As far as I know, this trick of replacing $\zeta(s)$ by $(1-2^{-s+1})^{-1}\zeta(s)$ is due to Euler, and it is a now standard method for replacing $\zeta(s)$ by a function which carries the same information, but does not have a pole at $s = 1$. The evaluation of $\zeta(s)$ at negative integers by passing to $(1-2^{-s+1})\zeta(s)$ and then performing Abelian regularization as above is also due to Euler, I believe. It is easy to see the Bernoulli numbers appearing in this way, for example.

---

Of course, taken literally, the series $\sum_{n=1}^{\infty} n$ diverges to $+\infty$, so any attempt to assign it a finite value will involve some form of regularization. Analytic continuation of the $\zeta$-function is one form of regularization, and the Abelian regularization that Lubos Motl and I are making is another. I can't quote a precise theorem to this effect (although maybe others can), but with such a simple expression as $\sum_{n = 1}^{\infty} n,$ I'm reasonably confident that any sensible regularization will necessarily yield the same value of $\dfrac{-1}{12}$. (Lubos Motl makes the same assertion in his answer.)

Answer 3

What a great method! I tried a few... $$ \sum_{n = 1}^{\infty} \left(\frac{1}{(2 n)^{s}} - \frac{1}{(2 n - 1)^{s}}\right) = \zeta (s) \Bigl(2^{1 - s} - 1\Bigr) $$ put $s=-1$ to get $\sum_{n = 1}^{\infty} 1 = -\frac{1}{4}$

or $$ \sum_{n = 1}^{\infty} \left(\frac{1}{(2 n + 1)^{s}} - \frac{1}{(2 n)^{s}}\right) = \left(1 - 2^{1-s}\right)\zeta(s) - 1 $$ put $s=-1$ to get $\sum_{n = 1}^{\infty} 1 = -\frac{3}{4}$

Answer 4

Computation of $\boldsymbol{\zeta(-1)}$ Using Integration by Parts

Here is a direct computation of $\zeta(-1)$ taken from this answer:

Multiply equation $(1)$ from this answer by $x+1$, then integrate by parts twice, to get $$ \begin{align} (1-2^{1-x})\zeta(x)\Gamma(x+2) &=\int_0^\infty\frac{(x+1)xt^{x-1}}{e^t+1}\mathrm{d}t\\ &=\int_0^\infty\frac{(x+1)t^xe^t}{(e^t+1)^2}\mathrm{d}t\\ &=\int_0^\infty\frac{t^{x+1}(e^{2t}-e^t)}{(e^t+1)^3}\mathrm{d}t\tag{1} \end{align} $$ Now we can plug in $x=-1$ into $(1)$ to get $$ \begin{align} (1-2^2)\zeta(-1)\Gamma(1) &=\int_0^\infty\frac{e^{2t}-e^t}{(e^t+1)^3}\mathrm{d}t\\ &=\int_1^\infty\frac{u-1}{(u+1)^3}\mathrm{d}u\\ &=\int_1^\infty\left(\frac1{(u+1)^2}-\frac2{(u+1)^3}\right)\mathrm{d}u\\ &=\frac14\tag{2} \end{align} $$ Since $(1-2^2)\Gamma(1)=-3$, $(2)$ says that $$ \zeta(-1)=-\frac1{12}\tag{3} $$ Naively plugging $n=-1$ into $$ \zeta(n)=\frac1{1^n}+\frac1{2^n}+\frac1{3^n}+\dots\tag{4} $$ yields $$ -\frac1{12}=1+2+3+4+\dots\tag{5} $$ However, the series on the right of $(5)$ is obviously divergent by the Term Test.

---

Computation of $\boldsymbol{\zeta(-1)}$ Using Euler-Maclaurin Sum Formula

As is shown in $(10)$ from this answer, for $\mathrm{Re}(s)\lt3$, we have $$ \lim_{n\to\infty}\left(\sum_{k=1}^nk^s-\frac{n^{s+1}}{s+1}-\frac{n^s}2-\frac{s\,n^{s-1}}{12}\right)=\zeta(-s)\tag6 $$ Plugging in $s=1$, we get $$ \begin{align} \zeta(-1) &=\lim_{n\to\infty}\overbrace{\left(\sum_{k=1}^nk-\frac{n^2}2-\frac{n}2-\frac1{12}\right)}^{-\frac1{12}\text{ for all $n$}}\\ &=-\frac1{12}\tag7 \end{align} $$

Answer 5

[19/3/19] Update - ref. 3b1b - Visualizing the Riemann hypothesis and analytic continuation : https://youtu.be/sD0NjbwqlYw - this piece demonstrates utmost clarity on $\zeta(-1)$ evaluation.

---

:: An explanation of how this is true and why and where it is useful and significant is summarized in 24 by John Baez (as part of the 19/09/08 Rankin Lectures) and yes, indeed this is weird.

---

The following is the same Euler's method described by Luboš Motl and Matt E in the other answers.

Let us consider the infinite geometric progression " $1, x, x^2, x^3, x^4, \dots$ "

The sum of this progression can be found by the formula $S_\infty = \large \frac{a}{1-r}$,

$$\implies 1 + x + x^2 + x^3 + x^4 + \dots = \frac{1}{1-x}$$ Differentiating with respect to $x$, $$ \implies 0 + 1 + 2x + 3x^2 + 4x^3 + \dots = \frac{1}{(x-1)^2}$$ Let $x = -1$, (Note: In the LHS, you get the alternating counterpart of the natural numbers series) $$\implies 1-2+3-4+5-6+...= \frac{1}{4} $$

$$ \bbox[5px,border:2px solid green]{\therefore \sum\limits_{i=1}^\infty n(-1)^{n-1} = \frac{1}{4}} $$

Subtracting this from $\sum\limits_{i=1}^\infty n$, $$\sum\limits_{i=1}^\infty n -\sum\limits_{i=1}^\infty n(-1)^{n-1} =4+8+12+...=4\sum\limits_{i=1}^\infty n$$ $$\implies 3\sum\limits_{i=1}^\infty n =-\sum\limits_{i=1}^\infty n(-1)^{n-1}=-1/4$$ $$\bbox[5px,border:2px solid lime]{\therefore \sum\limits_{i=1}^\infty n=-\frac{1}{12}}$$

---

This intuitive reasoning was made famous in a video by the physicist Phil Plait of Numberphile. It is heavily criticized for being sloppy but it shows a simple method that has fooled a large population of its high school audience (as noted in the comments).

---

Funfact: Googling -1/12 doesn't give you any results

Answer 6

If the following were true: $$\sum_{n=1}^\infty{n}=-\frac1{12}\tag{hypothesis}$$ then we would expect the following: $$\lim_{n\to\infty}\sum_{i=1}^n{i}\\ =\lim_{n\to\infty}\frac{n(n+1)}2=-\frac1{12}\tag{expectation}$$ which is the formula for the infinite triangular number limit. Unfortunately this is a result that we do not get when the limit is correctly taken. The correct value is $$\lim_{n\to\infty}\frac{n(n+1)}{2}\\ =\lim_{n\to\infty}\frac{n^2+n}{2}\\ =\lim_{m:{n^2+n}\to\infty}\frac{m}{2}=\infty\\ \neq-\frac{1}{12}$$ This sort of mathematical sleight of hand, smoke and mirrors, pulling a finite negative rabbit out of an empty positively infinite hat does not impress me; worse yet, it gives legitimate, observable, repeatable mathematics a bad name.

Answer 7

This infinite series is ultimately divergent because $$ 1+2+3+4+\cdots=\sum\limits_{k=1}^{\infty} k$$ $$ = \lim\limits_{n\to\infty} \sum\limits_{k=1}^{n} k = \lim\limits_{n\to\infty} \frac{n(n+1)}{2} = \infty $$ The value of $-\frac{1}{12}$ is attained by applying a different summability method, such as zeta function regularization and several others. If you'd like to understand how a divergent series can report a finite value by applying a different summability method, then have a look at this question.

Answer 8

The notation "$1+2+3+\cdots$" is as meaningless as "$1/0$". If you treat such notation as though it defined a real number and conformed in its syntax to the rules of formation for genuine real numbers, you can easily "prove" it to equal any number you like, including $-1/12$.

Answer 9

I am missing here that

$$1+2+3+\cdots \rightarrow \infty$$

$$\zeta(-1) \neq 1+2+3+\cdots$$

As you say, we only define $\zeta$ using the infinite sum if $\Re(s)>1$.

---

It is just as defining $$f(x) = \begin{cases} \frac{1}{x} &\mathrm{if} \; x \neq 0 \\ 0 & \mathrm{if} \; x = 0 \end{cases}$$

And asking why $f(0)=0$.

Answer 10

A nice alternative representation, by a double sum.

Consider the infinite square array where the rowsums and the (formal) column-sums are also given in closed forms $$ \small \begin{array} {r|rrrrr|rr} & & & & & & \text{rowsums} \\ \hline & 1/0! & \log(1)/1! & \log(1)^2/2! &\log(1)^3/3! & \cdots & = e^{\log(1)}&=1 \\ & 1/0! & \log(2)/1! & \log(2)^2/2! &\log(2)^3/3! & \cdots & = e^{\log(2)}&=2 \\ & 1/0! & \log(3)/1! & \log(3)^2/2! &\log(3)^3/3! & \cdots & = e^{\log(3)}&=3 \\ & \vdots & & & & \ddots & \vdots & \vdots\\ \hline \text{colsums:} & \zeta(0) & -\zeta(0)'/1! & \zeta(0)''/2!& -\zeta(0)^{(3)}/3! & \cdots &&=\zeta(-1) \end{array} $$ and the row-sum of the derivatives of the $\zeta()$ at $0$ in the bottom row can numerically be written as $$ \small -0.5 +0.9189... -1.003178...+1.000785...-0.999879...+1.0000019... \pm \cdots $$ If we split the terms and do two series we find $$ \Tiny \begin{array} {} -1 &+1 &-1 &+1 &-1 &+1 &\pm &\cdots &=-1/2\\ +0.5 &-0.0810... &-0.003178...&+0.000785...&+0.000120...&+0.0000019... &\pm &\cdots &= 5/12\\ \end{array}$$ Here we must now resort to the earlier definition of the divergent sum of the alternating units (in the first row), but the second row is convergent and can conventionally be summed. The sum of the two rowsums $\small -1/2 + 5/12 = -1/12$ gives the expected result.

However, that fiddling with double-sums, when non-convergent-series are involved (as are the columnsums in the above matrix and the splitting in the numerical expression) must explicitely be justified as "legal"/algebraically consistent operation.
But because I encounter it not frequently, that such non-convergent double-sum schemes come out with the expected result without further ado, I think this is a specific nice observation here.

And the more algebraically manipulations come out to be consistent with the assumed value of a divergent series, the more is the hypothese acceptable, that this should be taken as the canonical numerical replacement for the series-expression ( like we do it with the rational fraction for the geometric series even in the divergent case (except for that with quotient $q=1$)) .

Answer 11

Suppose a rigorous way of doing a computation yields a well defined real number as the answer. But with shortcut formal manipulations that are not allowed (e.g. interchanging summations and integrations when that isn't allowed) one ends up with a divergent series and then the question is that given only the divergent series, can one guess what real number is most likely the answer to what the unknown original problem was.

This is similar to guessing that the next term of the integer sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 is probably 16 rather than e.g. 32431, even though the latter possibility cannot be ruled out. Strictly speaking this problem is not well defined, what one really is doing here is assuming that the sequence that is specified by the least amount of information is the most likely answer. The person who invented the puzzle had some simple algorithm in mind, therefore the much more complicated algorithm that would yield 32431 as the next number in the sequence is not the likely answer.

Similarly, the formal manipulations that yield the divergent series won't have introduced a lot of additional information, these are just generic mathematical manipulations that would have been correct when used in a wide class of problems, but not the one it actually has been applied to. This means that almost all the information about the unknown real number is present in the divergent series, it can be extracted from it by applying certain formal manipulations to the series that, like the unknown manipulations that led to the divergent series, are formally correct for a wide class of convergent series, but not in case of this divergent series.

Answer 12

Euler's approach, but using algebra instead of subtraction of infinite series: Let $f(x)=(1-x)^{-2}$. Then $f(-x) = f(x) -4xf(x^2)$. Plug $x=1$ to get $f(-1)=-3f(1)$, whence $f(1)=-1/12$.

EDIT: This argument is a motivation for the mysterious value $-1/12$. Yes, $f(x) :=(1-x)^{-2}$ is undefined at $x=1$. If we define $f(1)=-1/12$, then the above identity holds for all $x$.

Answer 13

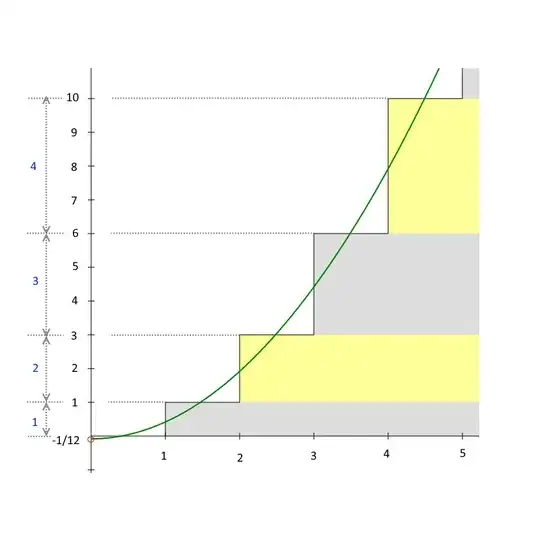
I like this simple graphical explanation.

There are first partial sums of the series 1 + 2 + 3 + 4 + ⋯ on picture. The parabola is their smoothed asymptote; its y-intercept is −1/12.

Answer 14

As I recently showed in another answer, we have the wonderful pattern:

$$\sum_{k=1}^n1=n\implies\int_{-1}^0x~\mathrm dx=\zeta(0)\\\sum_{k=1}^nk=\frac{n(n+1)}2\implies\int_{-1}^0\frac{x(x+1)}2~\mathrm dx=\zeta(-1)\\\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}6\implies\int_{-1}^0\frac{x(x+1)(2x+1)}6~\mathrm dx=\zeta(-2)\\\sum_{k=1}^nk^3=\left[\frac{n(n+1)}2\right]^2\implies\int_{-1}^0\left[\frac{x(x+1)}2\right]^2~\mathrm dx=\zeta(-3)\\\vdots$$

This pattern works for all $\zeta(-k)$.

Answer 15

Here is a useful place for Euler's transform and the Dirichlet eta function:

$$\zeta(s)=\sum_{n=1}^\infty\frac1{n^s}$$

$$\eta(s)=\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^s}$$

$$\zeta(s)-\eta(s)=\sum_{n=1}^\infty\frac{1+(-1)^n}{n^s}=\sum_{n=1}^\infty\frac2{(2n)^s}=2^{1-s}\sum_{n=1}^\infty\frac1{n^s}=2^{1-s}\zeta(s)$$

$$\zeta(s)-\eta(s)=2^{1-s}\zeta(s)\implies (1-2^{1-s})\zeta(s)=\eta(s)$$

$$\zeta(s)=\frac1{1-2^{1-s}}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^s}$$

After a quick application of Euler's transform, we get a nice analytic continuation to the entire complex plane.

$${\small E_1}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^s}=\sum_{n=0}^\infty\left[\frac1{2^{n+1}}\sum_{k=0}^n\binom nk\frac{(-1)^k}{(k+1)^s}\right]$$

Finally giving us

$$\zeta(s)=\frac1{1-2^{1-s}}\sum_{n=0}^\infty\left[\frac1{2^{n+1}}\sum_{k=0}^n\binom nk\frac{(-1)^k}{(k+1)^s}\right]$$

And at $s=-1$,

$$\zeta(-1)=-\frac1{12}$$