Apparently $1+2+3+4+\ldots+n = \dfrac{n\times(n+1)}2$.
How? What's the proof? Or maybe it is self apparent just looking at the above?
PS: This problem is known as "The sum of the first $n$ positive integers".
Apparently $1+2+3+4+\ldots+n = \dfrac{n\times(n+1)}2$.
How? What's the proof? Or maybe it is self apparent just looking at the above?
PS: This problem is known as "The sum of the first $n$ positive integers".
Let $$S = 1 + 2 + \ldots + (n-1) + n.$$ Write it backwards: $$S = n + (n-1) + \ldots + 2 + 1.$$ Add the two equations, term by term; each term is $n+1,$ so $$2S = (n+1) + (n+1) + \ldots + (n+1) = n(n+1).$$ Divide by 2: $$S = \frac{n(n+1)}{2}.$$
My favourite proof is the one given here on MathOverflow. I'm copying the picture here for easy reference, but full credit goes to Mariano Suárez-Alvarez for this answer.
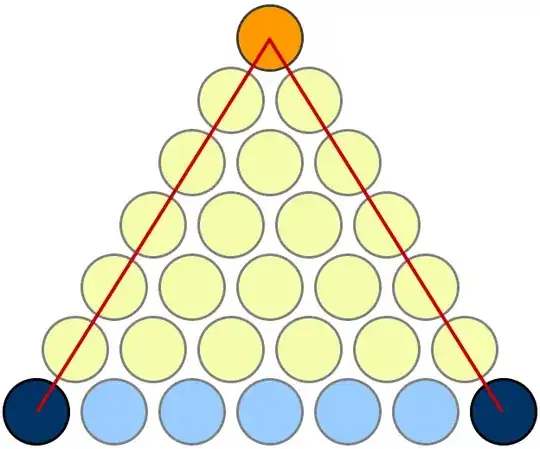
Takes a little bit of looking at it to see what's going on, but it's nice once you get it. Observe that if there are n rows of yellow discs, then:
What a big sum! This is one of those questions that have dozens of proofs because of their utility and instructional use. I present my two favorite proofs: one because of its simplicity, and one because I came up with it on my own (that is, before seeing others do it - it's known).
The first involves the above picture: 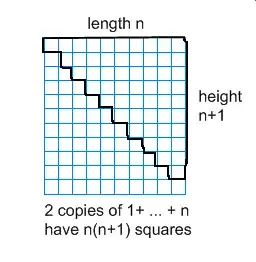
In short, note that we want to know how many boxes are in the outlined region, as the first column has 1 box, the second 2, and so on (1 + 2 + ... + n). One way to count this quickly is to take another copy of this section and attach it below, making a $n*(n+1)$ box that has exactly twice as many squares as we actually want. But there are $n*(n+1)$ little squares in this area, so our sum is half that: $$ 1 + 2 + ... + n = \dfrac{n(n+1)}{2}. $$
Second proof, same as the first but a little bit harder and a little bit worse:
Let us take for granted the finite geometric sum $1 + x + x^2 + ... + x^n = \dfrac{x^{n+1} - 1}{x-1}$ (If you are unfamiliar with this, comment and I'll direct you to a proof). This is a polynomial - so let's differentiate it. We get $$ 1 + 2x + 3x^2 + ... + nx^{n-1} = \dfrac{ (n+1)x^n (x-1) - x^{n+1} + 1}{ (x-1)^2 }$$ Taking the limit as x approaches 1, we get
$$ \lim_{x \to 1} \dfrac{ (n+1)x^n (x-1) - x^{n+1} + 1}{ (x-1)^2} = \dfrac{ (n+1) [ (n+1)x^n - nx^{n-1} ] - (n+1)x^n }{2(x-1)} = $$ $$ \lim_{x \to 1} \dfrac{ (n+1)[(n+1)(n)x^{n-1} - n(n-1)x^{n-2}] - (n+1)(n)x^{n-1} } {2}$$
where we used two applications of l'Hopital above. This limit exists, and plugging in x = 1 we see that we get $$ \dfrac{1}{2} * (n+1)(n) [ (n+1) - (n-1) - 1] = \dfrac{ (n)(n+1)}{2}.$$
And that concludes the second proof.
How many ways are there to choose a $2$-element subset out of an $n$-element set?
On the one hand, you can choose the first element of the set in $n$ ways, then the second element of the set in $n-1$ ways, then divide by $2$ because it doesn't matter which you choose first and which you choose second. This gives $\frac{n(n-1)}{2}$ ways.
On the other hand, suppose the $n$ elements are $1, 2, 3, ... n$, and suppose the larger of the two elements you choose is $j$. Then for every $j$ between $2$ and $n$ there are $j-1$ possible choices of the smaller of the two elements, which can be any of $1, 2, ... j-1$. This gives $1 + 2 + ... + (n-1)$ ways.
Since the two expressions above count the same thing, they must be equal. This is known as the principle of double counting, and it is one of a combinatorialist's favorite weapons. A generalization of this argument allows one to deduce the sum of the first $n$ squares, cubes, fourth powers...
Gathering as many proofs as we can? Write the series recursively:
$$S(n) = S(n - 1) + n \tag{1}$$
Substitute $n \to n+1$ :
$$S(n + 1) = S(n) + n + 1\tag{2}$$
Equation (2) subtract Equation (1):
$$S(n+1) - S(n) = S(n) + 1 - S(n - 1) \tag{3}$$
And write it up:
$$\begin{cases} S(n+1) &= 2S(n) -S(n-1) + 1 \\ S(n) &= S(n) \end{cases} \tag{4}$$
Which can now be written in matrix form:
$$ \begin{bmatrix} S(n+1) \\ S(n) \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} S(n) \\ S(n-1) \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \end{bmatrix} \tag{5}$$
And then converting the affine equation (5) to the linear equation (6):
$$ \begin{bmatrix} S(n+1) \\ S(n+0) \\ 1\end{bmatrix} = \begin{bmatrix} 2 & -1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} S(n) \\ S(n-1) \\ 1\end{bmatrix} \tag{6}$$
And closing the equation:
$$ \begin{bmatrix} S(n+1) \\ S(n) \\ 1\end{bmatrix} = \begin{bmatrix} 2 & -1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix}^n \begin{bmatrix} S(1) \\ S(0) \\ 1\end{bmatrix} \tag{6}$$
Then finding the Jordan form of the 3x3 matrix:
$$\begin{align} \begin{bmatrix} S(n+1) \\ S(n) \\ 1\end{bmatrix} &= \left(\begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix}^{-1}\right)^n \begin{bmatrix} S(1) \\ S(0) \\ 1\end{bmatrix} \\ &= \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1\end{bmatrix}^n \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix}^{-1} \begin{bmatrix} S(1) \\ S(0) \\ 1\end{bmatrix} \\ &= \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 1 & \binom{n}{1} & \binom{n-1}{2} \\ 0 & 1 & \binom{n}{1} \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 0 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} S(1) \\ S(0) \\ 1\end{bmatrix} \end{align} \tag{7}$$
And multiplying the matrices out:
$$\begin{bmatrix} S(n+1) \\ S(n) \\ 1\end{bmatrix} = \begin{bmatrix} \frac{ (2n+2)S(1) - 2nS(0) + {n}^{2} + n}{2} \\ \frac{ 2nS(1) + (2 - 2n)S(0)+{n}^{2}-n}{2} \\ 1 \end{bmatrix} \tag{8}$$
And given that $S(0) = 0$ and $S(1) = 1$, we get that:
$$S(n) = \frac{n^2 + n}{2} \tag{9}$$
My favourite proof of this fact involves counting the edges of the complete graph $K_n$ in two different ways.

On the one hand, any vertex, $v_1$ say, is connected to $n-1$ other vertices, thus contributing $n-1$ edges. Moving clockwise, the next vertex $v_2$ contributes $n-2$ edges (not counting the edge connecting $v_1$ and $v_2$), $v_3$ adds $n-3$ edges, ... , $v_{n-1}$ contributes 1 edge and $v_n$ adds no new edges.
Thus the total number of edges in the complete graph $K_n$ is:
$$E = \sum\limits_{i=1}^{n-1} i$$
But clearly, any edge connects two vertices, so the number of edges is the number of ways to choose two distinct elements from the set $\{1,...,n\}$ and hence:
$$E = \sum\limits_{i=1}^{n-1} i = \binom{n}{2} = \frac{n(n-1)}{2}$$
For example, $$X = 1+2+3+4+5+6$$ Then twice $X$ is $$2X = (1+2+3+4+5+6) + (1+2+3+4+5+6)$$ which we can rearrange as $$2X = (1+2+3+4+5+6) + (6+5+4+3+2+1)$$ and add term by term to get $$2X = (1+6)+(2+5)+(3+4)+(4+3)+(5+2)+(6+1)$$ to get $$2X = 7+7+7+7+7+7 = 6*7 = 42$$
Once you have a formula like this, you can prove it by induction. But that begs the question as to how you get such a formula. In this case you might ask: (a) what's the "average" term? and (b) how many terms are there?
If you knew of the geometric series, you would know that
$$\frac{1-r^{n+1}}{1-r}=1+r+r^2+r^3+\dots+r^n$$
If we differentiate both sides, we have
$$\frac{nr^{n+2}-(n+1)r^{n+1}+r}{(1-r)^2}=1+2r+3r^2+\dots+nr^{n-1}$$
Letting $r\to1$ and applying L'Hospital's rule on the fraction, we end up with
$$\frac{n(n+1)}2=1+2+3+\dots+n$$
HINT Pair each summand $k$ with its "reflection" $n+1-k$. This is simply a discrete analog of the method of computing the area of the triangle under the diagonal of a square by reflecting a subtriangle through the midpoint of the diagonal to form an $n$ by $n/2$ rectangle.
Like the analogous proof of Wilson's theorem, the method exploits the existence of a nontrivial symmetry. In Wilson's theorem we exploit the symmetry $n \mapsto n^{-1}$ which exists due to the fact that ${\mathbb F}_p^*$ forms a group. Here we exploit a reflection through a line - a symmetry that exists due to the linear nature of the problem (which doesn't work for nonlinear sums, e.g. $\sum n^2$). Symmetries often lead to elegant proofs. One should always look for innate symmetries when first pondering problems.
Generally there are (Galois) theories and algorithms for summation in closed form, in analogy to the differential case (Ritt, Kolchin, Risch et al.). A very nice motivated introduction can be found in the introductory chapter of Carsten Schneider's thesis Symbolic Summation in Difference Fields.
Draw a triangular pyramid of base $n+1$. We get a unique coordinate for any of the $\sum_{i=1}^ni$ elements of the pyramid not in the bottom row by choosing two of the elements in the bottom row of $n+1$. This gives a bijection from the $\binom{n+1}{2}$ coordinate pairs to the $\sum_{i=1}^ni$ elements of the pyramid not in the bottom row.
Image from Mariano Suárez-Alvarez's answer on Math Overflow:
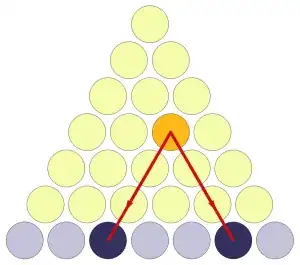
Basically same proof as Yoyo's, just purely combinatorial (no picture needed):
How many ways can we chose two distinct numbers between $1$ and $n+1$?
We pick first the largest, which is of the form $i+1$ for some $1 \leq i \leq n$, and then we have exactly $i$ distinct choices for the smallest one.
Thus we have $\sum_{i=1}^n i$ choices.
Here is another idea:
Using $(i+1)^2-i^2=2i+1$ we get a telescopic sum:
$$ \sum_{i=1}^n (2i+1) = \sum_{i=1}^n ((i+1)^2-i^2) = (n+1)^2-1=n^2+2n \,.$$
Then
$$n^2+2n= 2\left[\sum_{i=1}^n i\right] +n \,.$$
Let us denote the sum as $S_1(n)$. This function must be a second degree polynomial in $n$ because the first order difference $S_1(n)-S_1(n-1)=n$ is a linear polynomial in $n$. So it suffices to construct the Lagrangian polynomial by three known points, let $(0,0), (1,1), (2,3)$.
$$S_1(n)=0\frac{(n-1)(n-2)}{(0-1)(0-2)}+1\frac{(n-0)(n-2)}{(1-0)(1-2)}+3\frac{(n-0)(n-1)}{(2-0)(2-1)}=\frac{n(n+1)}2.$$
With the Euler-Maclaurin summation formula, one can easily derive that
$$\sum_{k=1}^nk=\int_0^nx\ dx+\frac12n=\frac12n^2+\frac12n$$
More generally, one may derive that
$$\sum_{k=1}^n k^p = {1 \over p+1} \sum_{j=0}^p (-1)^j{p+1 \choose j} B_j n^{p+1-j},\qquad \mbox{where}~B_1 = -\frac{1}{2}$$
where we use the Bernoulli numbers. This more general formula is more commonly known as Faulhaber's formula.
Here is an easy way to visualize it:
Draw a rectangular grid with a height of $n$ squares and width of $n+1$ squares. Obviously it has $n(n+1)$ squares in it.
In the first row, color the leftmost square red and the other $n$ squares blue; in the second row, color the leftmost $2$ squares red and the other $n-1$ squares blue; and so forth (in the last row, there will be $n$ red squares and one blue square). Clearly, there are $\sum_{i=1}^n i$ red squares and the same number of blue squares.
Adding the red and blue squares together, we get $2 \sum_{i=1}^n i = n(n+1)$, or $\sum_{i=1}^n i = n(n+1)/2$.
You can take the power series
$$f(x)=\sum_{n=0}^\infty\left(\sum_{j=0}^{n}j\right)x^n$$
and you can check that it has a postive convergence ratio, and changing the order of the series you can deduce that
$$f(x)=\frac{x}{(1-x)^3}.$$
On the other hand the taylor series for $\frac{x}{(1-x)^3}$ is precisely
$$\frac{x}{(1-x)^3}=\sum_{n=0}^\infty \frac{n(n+1)}{2}x^n$$
so $$\sum_{j=0}^nj=\frac{n(n+1)}{2}.$$
$\dfrac{k+1}2-\dfrac{k-1}2=1 \implies\dfrac{k(k+1)}2-\dfrac{(k-1)k}2=k$
$\implies \sum_{k=1}^n\Bigg(\dfrac{k(k+1)}2-\dfrac{(k-1)k}2\Bigg)=\sum_{k=1}^nk\implies\dfrac{n(n+1)}2-\dfrac{1(1-1)}2=\sum_{k=1}^nk$
$\implies\sum_{k=1}^nk=\dfrac{n(n+1)}2$
Let us denote the sum as $S_1(n)$. This function must be a second degree polynomial in $n$ because the first order difference $S_1(n)-S_1(n-1)=n$ is a linear polynomial in $n$. So it suffices to verify the formula for three different values of the argument.
$$S_1(0)=0=\frac{0(0+1)}2,$$ $$S_1(1)=1=\frac{1(1+1)}2,$$ $$S_1(2)=3=\frac{2(2+1)}2.$$ QED.
I didn't see an answer using the method that I used, so I'm posting an answer here to 'spread the knowledge!'
This can be applied to higher powers such $1^2+2^2+\cdots n^2$ or $1^3+2^3+\cdots n^3$.
Solving by the use of Indeterminate Coefficients:
Assume the series$$1+2+3+4+5\ldots+n\tag1$$ Is equal to the infinite series$$1+2+3+4+5+\ldots+n=A+Bn+Cn^2+Dn^3+En^4+\ldots\&c\tag2$$ If we 'replace' $n$ with $n+1$, we get$$1+2+3+4+\ldots+(n+1)=A+B(n+1)+C(n+1)^2+\ldots\&c\tag3$$ And subtracting $(3)-(2)$, gives$$\begin{align*} & n+1=B+C(2n+1)\tag4\\n & +1=2Cn+(B+C)\tag5\end{align*}$$ Therefore, $C=\dfrac 12,B=\dfrac 12,A=0$ and $(1)$ becomes$$1+2+3+4+5\ldots+n=\dfrac n2+\dfrac {n^2}2=\dfrac {n(n+1)}{2}$$
The most general case of this is called an arithmetic progression or (finite) arithmetic series. There are many, many, many proofs. An easy one: write all the summands in a row; write them again just below, but from right to left now (so $1$ is under $n$, $2$ is under $n-1$, etc). Add them up, and figure out how it relates to the quantity you are looking for.
Another "picture proof" I just thought of... but without a picture, since I can't draw:
Suppose you want to add up all the integers from 1 to n. Then draw n rows on a board, put 1 unit in the first row, 2 in the second, and so on. If you draw a right triangle of height and length n to try and contain this shape, you will cut off half of each unit on the diagonal. So let's add all of these up; you have $n^2/2$ units inside the triangle, and you have $n/2$ units cut off on the diagonal (there are n squares on the diagonal, and half of each one is cut off). Adding these gives $n^2/2 + n/2 = n(n+1)/2$.
If you draw it out, it makes more sense, and I think it's geometrically a bit more straightforward than the other picture proof.
(Side note: I have no idea how to write math on this site... I'll go consult the meta, I'm sure there's something there about it.)
Some time ago I saw someone explain it as follows:
The average value of $1,2,3,\dots,n$ is simply $\frac{n+1}2$. Thus $1+2+3+\dots+n=\frac{n(n+1)}2$.
Of course the proof behind this leads to Gauss's proof quite directly, but nonetheless I really like this restatement of it as it is easy to understand even if one does not know much math. And it quickly gives the sum of terms in arithmetic progression as well. Such a sum is simply the number of terms times the average of the first and last terms.
Here are two ways to calculate this sum. First is by symmetry of another sum:
$\begin{aligned} \displaystyle & \sum_{0 \le k \le n}k^2 = \sum_{0 \le k \le n}(n-k)^2 = n^2\sum_{0 \le k \le n}-2n\sum_{0 \le k \le n}k+\sum_{0 \le k \le n}k^2 \\& \implies 2n\sum_{0 \le k \le n}k = n^2(n+1) \implies \sum_{0 \le k \le n}k = \frac{1}{2}n(n+1).\end{aligned}$
The second is writing it as double sum and switching the order of summation:
$\begin{aligned}\displaystyle & \begin{aligned}\sum_{1 \le k \le n}k & = \sum_{1 \le k \le n}~\sum_{1 \le r \le k} = \sum_{1 \le r \le n} ~\sum_{r \le k \le n} = \sum_{1 \le r \le n}\bigg(\sum_{1 \le k \le n}-\sum_{1 \le k \le r-1}\bigg) \\& =\sum_{1 \le r \le n}\bigg(n-r+1\bigg) = n\sum_{1 \le k \le n}-\sum_{1 \le k \le n}k+\sum_{1 \le k \le n}\end{aligned} \\& \implies 2\sum_{1 \le k \le n}k = n^2+n \implies \sum_{1 \le k \le n}k = \frac{1}{2}n(n+1), ~ \mathbb{Q. E. D.} \end{aligned}$
Note I started using k back on the third line for convenience because r is just a dummy vairable at this point, and our sum no longer depends on k. Note that the first trick can easily be generalised:
$\begin{aligned} & \hspace{0.5in}\begin{aligned}\displaystyle \sum_{0 \le k \le n}k^{2p} &= \sum_{0 \le k \le n}(n-k)^{2p} \\& = \sum_{0 \le k \le n}~\sum_{0 \le r \le 2p}\binom{2p}{r}n^r(-1)^{2p-r}k^{2p-r}\\& = \sum_{0 \le k \le n}k^{2p}-2pn\sum_{0 \le k \le n}k^{2p-1}+\sum_{0 \le k \le n}~\sum_{2 \le r \le 2p}\binom{2p}{r}n^r(-1)^{2p-r}k^{2p-r} \end{aligned} \\& \implies \sum_{0 \le k \le n}k^{2p-1} = \frac{1}{2pn}\sum_{0 \le k \le n}~\sum_{2 \le r \le 2p}\binom{2p}{r}n^r(-1)^{2p-r}k^{2p-r}. \end{aligned}$
$$\sum_{i=0}^ni-\sum_{i=0}^{n-1}i=S_1(n)-S_1(n-1)=n,$$ so that $S_1(n)$ must be a polynomial of the second degree in $n$. By the method of undeterminate coefficients, noting that there is no constant term as $S_1(0)=0$: $$S_1(n)-S_1(n-1)=n=(an^2+bn)-(a(n-1)^2+b(n-1))=\\=2an+b-a,$$ and by identification $$a=b=\frac12.$$ $$S_1(n)=\frac{n^2+n}2.$$ Let us generalize to the sum of squares, $$S_2(n)-S_2(n-1)=n^2=(an^3+bn^2+cn)-(a(n-1)^3+b(n-1)^2+c(n-1))=\\=3an^2+(-3a+2b)n+a-b+c,$$ giving $$a=\frac13,b=\frac12,c=\frac16.$$ $$S_2(n)=\frac{2n^3+3n^2+n}6.$$ For any power, you get a triangular system of equations where you recognize a part of Pascal's triangle, with alternating signs, as in the sum of cubes: $$S_3(n)-S_3(n-1)=n^3=4an^3+(-6a+3b)n^2+(4a-3b+2c)n+(-a+b-c+d),$$ $$\color{blue}{4}a=1\\-\color{blue}{6}a+\color{blue}{3}b=0\\\color{blue}{4}a-\color{blue}{3}b+\color{blue}{2}c=0\\-\color{blue}{1}a\ +\color{blue}{1}b-\color{blue}{1}c+\color{blue}{1}d=0,$$ giving $$a=\frac14,b=\frac12,c=\frac14,d=0.$$ $$S_3(n)=\frac{n^4+2n^3+n^2}4.$$

Above is an image representing Pascals Triangle. What I want to draw attention to is the hockey stick formation, particularly, the blue hockey stick. Notice how the entries in the stick of the blue hockey stick are in arithmetic progression, and that the entry in the blade represents the sum of the entries in the stick.
To prove this inductively we have as a bootstrap condition
$$1=\frac{1(1+1)}{2}=\binom{1+1}{2} = \sum\limits_{i=1}^1\binom{i}{1}=1$$
and for the general case
$$\begin{array}{lll} \sum\limits_{i=1}^{n+1}&=&(n+1)+\sum\limits_{i=1}^{n}i\\ &=&\binom{n+1}{1}+\binom{n+1}{2}\\ &=&\binom{n+2}{2}\\ &=&\binom{(n+1)+1}{2}\\ &=&\frac{(n+1)((n+1)+1)}{2} \end{array}$$
Of course, we assumed that $\binom{n}{k}+\binom{n}{k+1} = \binom{n+1}{k+1}$ holds. $$\begin{array}{lll} \binom{n}{k}+\binom{n}{k+1}&=&\frac{n!}{k!(n-k)!} + \frac{n!}{(k+1)!(n-(k+1))!}\\ &=&\frac{n!(k+1)}{k!(k+1)(n-k)!} + \frac{n!(n-k)}{(k+1)!(n-(k+1))!(n-k)}\\ &=&\frac{n!k+n!+n!n-n!k}{(k+1)!(n-k)!}\\ &=&\frac{n!+n!n}{(k+1)!((n+1)-(k+1))!}\\ &=&\frac{n!(n+1)}{(k+1)!((n+1)-(k+1))!}\\ &=&\frac{(n+1)!}{(k+1)!((n+1)-(k+1))!}\\ &=&\binom{n+1}{k+1}\\ \end{array}$$
All these proofs seem very complicated. The way I remember it is:
The sequence is: 1, 2, 3, ..... (n-2), (n-1), n.
Taking the last and first term, 2nd and (n-2)th term and so on, we form n/2 pairs of (n+1). So the sum of n/2 pairs of (n+1) is n/2 * (n+1)
Example: 1, 2, 3, 4, 5, 6 = (1+6) + (2+5) + (3+4) = 3x7 =21
This still holds for an odd number of terms
I would like to resubmit the first 'backwards and forwards' proof above. My issue with the proof is the use of "$\dots$" which translates to and so on. Here is a more mathematically rigorous proof using properties of summation $\Sigma$. $$ 2\sum_{k=1}^{n} k =\sum_{k=1}^{n} 2k = \sum_{k=1}^{n} (k+k) = \sum_{k=1}^{n}k + \sum_{k=1}^{n}k = \sum_{k=1}^{n}k+ \sum_{k=1}^{n}(n-(k-1))= n(n+1) $$
The ordinary generating function for the sequence of all ones is $\frac1{1-x}$ and dividing an o.g.f. of a sequence by $1-x$ produces the o.g.f. for the sequence of partial sums of the first sequence, so the o.g.f. for $a_n=\sum_{k=1}^{n+1}k$ is $\frac1{(1-x)^3}$. Applying the Generalized Binomial Theorem, we therefore have $$1+2+\cdots+n = [x^{n-1}]\frac1{(1-x)^3} = (-1)^{n-1}\binom{-3}{n-1} = \binom{n+1}2 = \frac{n(n+1)}2.$$
You can also prove it by induction, which is nice and easy, although it doesn't give much intuition as to why it works.
It works for $1$ since $\frac{1\times 2}{2} = 1$.
Let it work for $n$.
$$1 + 2 + 3 + \dots + n + (n + 1) = \frac{n(n+1)}{2} + (n + 1) = \frac{n(n+1) + 2(n+1)}{2} = \frac{(n+1)(n+2)}{2}.$$
Therefore, if it works for $n$, it works for $n + 1$. Hence, it works for all natural numbers.
For the record, you can see this by applying the formula for the sum of an arithmetic progression (a sequence formed by constantly adding a rate to each term, in this case $1$). The formula is reached pretty much using the method outlined by Carl earlier in this post. Here it is, in all its glory:
$$S_n = \frac{(a_1 + a_n) * n}{2}$$
($a_1$ = first term, $a_n$ = last term, $n$ = number of terms being added).
I stumbled across this identity
$\quad ab - 1 = (a - 1) (b - 1) + (a - 1) + (b - 1)$
while working with modulo arithmetic a couple of days ago. I was upset that I couldn't use it in any (really) interesting ways, but now I've discovered that I can 'pile onto' this question!
If $n \ge 1$ is an integer we can write
$\tag 1 n^2 = (n - 1)^2 + 2 (n - 1) + 1$
Observe that the first term of the rhs of $\text{(1)}$ is the square of an integer, just like the lhs of $\text{(1)}$. So you can use 'downward finite induction formula recursion' (not sure what to call this) and conclude that
$\quad n^2 = [\displaystyle 2 \sum_{k=1}^{n-1}\, k] + n$
and this even holds for $n = 1$.
Rewriting the formula we obtain
$\quad \displaystyle \frac{n(n-1)}{2} = \sum_{k=1}^{n-1}\, k$
For a group of friends in a party, they like to shake hands with each other once in the following way:
Therefore the total times of shaking hands=$1+2+3+\cdots+(n-1)= \left(\begin{array}{l}n \\ 2\end{array}\right)$.
Well if we graph the numbers $1,2,3,4,.. $ we get a line. Graphing $(1,1)$, $(2,2)$, $(3,3)$ ...I mean. And these numbers occur in a linear fashion so the average of these numbers from $1$ to $n$ is $\frac{n+1}{2}$ and we multiply that by $n$ numbers. Pretty cool huh?
Maybe this one will interest you too:
$$1+3+5+7+9....+(2n-1)=n^2$$
Three answers by Yves Daoust, this one, this one, and this one, are based on demonstrating that the answer is a second degree polynomial in $n$. In this answer I'm going to derive the formula based on that fact plus a reflection formula that the analytic continuation of the polynomial satisfies. The argument also works well to constrain the functional form of summations of integer powers, so let's consider the function $S(n,r)$, defined as
$$S(n,r) = \sum_{k=0}^{n}k^r\tag{1}.$$
This is then a polynomial of degree $r+1$, but note that Eq. (1) makes sense only for integer values of $n$. But because we know that this $S(n,r)$ is a polynomial, we can define $S(n,r)$ for any arbitrary complex value of $n$ as the value taken by the polynomial there.
Let's start by extending $S(n,r)$ to negative integer $n$. The summation with a general lower limit can be written as
$$\sum_{k=n}^m k^r = S(m,r) - S(n-1,r).$$
We then demand that this is valid even if the first argument of $S$ is negative. We can then write for $n\geq 0$
$$\sum_{k=-n}^0 k^r = -S(-n-1,r)$$
Since
$$\sum_{k=-n}^0 k^r = (-1)^r S(n,r)$$
we have
$$S(-n-1,r) = (-1)^{r+1} S(n,r)\tag{2}.$$
This implies that $S(0,r) = S(-1,r) = 0$. This then fixes $S(n,1)$ up to an overall factor. From this answer by Simply Beautiful Art, we can see that the overall factor can be obtained from the leading asymptotic behavior
$$S(n,r) =\frac{n^{r+1}}{r+1} + \mathcal{O}{(n^r)}\tag{3}.$$
So, we have
$$S(n,1) = \frac{1}{2}n(n+1).$$
The sum of squares also follows almost immediately from Eq.(2), as this implies that $S(n,2)$ is an odd function of $2n+1$, and must thus contain a factor of $2n+1$ besides the factors of $n$ and $n+1$. Since $S(n,2)$ is a third degree polynomial this again fixes the function up to an overall factor. Using Eq.(3), we then find
$$S(n,2) = \frac{1}{6}n (n+1)(2n+1).$$
Many good answers; I add a proof of the formula by induction.
Defining $T(n) = \sum_{i=1}^n i$, the claim is that $T(n) = n(n+1)/2$
For the base case of $n=1$, the sum gives us that $T(n) = 1$ and $n(n+1)/2 = 2/2 = 1$ $\quad \color{#0B2}\checkmark$
Assuming the inductive hypothesis that $T(k)=k(k+1)/2$, we have:
$$\begin{align} T(k{+}1) &= \sum_{i=1}^{k+1} i \\ &= \sum_{i=1}^{k} i \;+ k{+}1\\ &= k(k+1)/2 \;+ k{+}1 \\ &= k(k+1)/2 \;+ 2(k+1)/2 \\ &= (k+2)(k+1)/2 \\ &= (k{+}1)((k{+}1)+1)/2 \quad \color{#0B2}\checkmark \\ \end{align}$$ as required to completion the induction.