Easy example why complex numbers are cool

Question

I am looking for an example explainable to someone only knowing high school mathematics why complex numbers are necessary. The best example would be possible to explain rigourously and also be clearly important in a daily day sense.

I.e. complex Laplace transform has applications in pricing of options in mathematical finance which is somewhat easy to sell as important, but impossible to explain the details of.
It is easy to say: Then we can generalise the square root! - but it is harder to argue why that makes any difference in the real world.

The question has edited the wording cool out of it replaced with a description to stop it from being opinion based. I hope it helps :)

Answer 1

Using $e^{i\theta} = \cos \theta + i \sin \theta$ it is very easy to find (and remember) many trigonometric identities.

For example, $e^{i(\alpha+\beta)} = e^{i\alpha}e^{i\beta}$ gives the sine-of-sums and cosine-of-sums formulas.

---

$$ \begin{align} e^{i(\alpha+\beta)} &= e^{i\alpha}e^{i\beta} \\ \cos(\alpha+\beta) + i \sin(\alpha+\beta) &= (\cos \alpha + i \sin \alpha)(\cos \beta + i \sin \beta) \\ &= (\cos \alpha \cos \beta - \sin \alpha \sin \beta) + i (\sin \alpha \cos \beta + \cos \alpha \sin \beta) \\ \end{align} $$

Equating the real parts,

$$\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$$

Equating the imaginary parts,

$$\sin(\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$

Answer 2

Here's a really cool application: Complex Step Differentiation

The basic idea is that you normally compute a derivative as:

$$f'(x) \approx \frac{f(x+h)-f(x)}{h}$$

This requires evaluating $f$ twice. But what if we use complex numbers?

$$f'(x) \approx \frac{f(x+ih)-f(x)}{ih}\approx \frac{\Im{f(x+ih)}}{ih} $$

Now we only need to evaluate $f$ once!* ($\Im(z)$ is just the imaginary part of $z$.)
Not just that, but it's a lot more numerically accurate, too -- see the link above.

_{* This assumes the function is real-valued for real inputs, and analytic. In practice it often is.}

Answer 3

Complex numbers are necessary for Cardano's formulae to work in all cases of the third degree equation: $x^3+px+q=0$. Setting $\Delta=4p^3+27q^2$, the root(s), if any, are given by

$$x=\sqrt[3]{\frac{1}{2}\Biggl(-q -\sqrt{\frac{\Delta}{27}}\Biggr)}+ \sqrt[3]{\frac{1}{2}\Biggl(-q +\sqrt{\frac{\Delta}{27}}\Biggr)}. $$

Now this formula works fine when there are 1 or 2 (real) roots, because it is the case when $\Delta \geq 0$. However the case of 3 real roots corresponds to the case $\Delta <0$ and hence, in order to use the formula, you need to use square roots of negative numbers.

The simplest example is the equation $x^3-7x+6=0$, which has 3 evident roots: 1, 2 and –3.

Answer 4

The solutions to $x^n=1$ are $n$ evenly spaced points around the unit circle.

For example, all 5 values of $x$ that satisfy $x^5=1$ are found at the points

(Image from Wikipedia.)

It is results such as this that motivate and justify the 2-dimensional representation of complex numbers by the complex plane.

Answer 5

Compare solving an electrical AC circuit with capacitors and inductors with complex quantities with any other method.

Generalizing resistance to impedance makes the whole computation just shuffling around a few numbers (which may or may not have any intuitive meaning), compared to doing essentially the same thing by, e.g., graphical methods.

Answer 6

Mandelbrot set http://en.wikipedia.org/wiki/Mandelbrot_set should be cool, however rather not easy to describe in a formal way. But if it can be done informally...

Answer 7

If your high school student has seen Taylor series, the following might work.

The Taylor series of $\frac{1}{1-x}$ about $x=0$ has radius of convergence $1$. This can be explicitly computed, but it also makes sense because of the pole at $x=1$.

It may come as a surprise that the $C^\infty$ function $\frac{1}{1+x^2}$ also has radius of convergence $1$. What is limiting the radius of convergence? Even though we are only asking "real" questions about a "real" function, it is the presence of poles at $x=i$ and $x=-i$ which dictates this behavior.

Similarly, $\frac{1}{1+e^x}$ has radius of convergence $\pi$, which can be explained with Euler's formula.

Answer 8

Every polynomial with real (or complex) coefficients has a complex root. This is the Fundamental Theorem of Algebra. The important fact here is that if we restrict to real numbers the root may not exist; complex numbers are required in general.

Answer 9

Your problem: factor $x^4 - 2$ over the real numbers.

Easy solution:

• Find its complex roots: they are $\sqrt[4]{2}$, $\mathbf{i}\sqrt[4]{2}$, $-\sqrt[4]{2}$, $-\mathbf{i}\sqrt[4]{2}$.
• Its factorization over the complexes is thus $$ (x-\sqrt[4]{2})(x-\mathbf{i}\sqrt[4]{2})(x+\sqrt[4]{2})(x+\mathbf{i}\sqrt[4]{2})$$
• Group them into real factors and complex conjugate pairs of factors $$ (x-\sqrt[4]{2})(x+\sqrt[4]{2})\left((x-\mathbf{i}\sqrt[4]{2})(x+\mathbf{i}\sqrt[4]{2})\right)$$
• Combine the complex conjugate pairs: $$ (x-\sqrt[4]{2})(x+\sqrt[4]{2})(x^2 + \sqrt{2}) $$

This general approach lets you factor any polynomial over the reals, particularly in a setting where you're doing calculations numerically.

Answer 10

How about the fact that $$e^{i\pi} +1 = 0?$$

That's one of the coolest equations around, because:

• It contains all elementary operations (exponentiation, multiplication and addition)
• It contains five important constants of mathematics ($e,\pi, i, 1$ and $0$)
• It's short and easy to memorise

Answer 11

I used to love using complex numbers to derive tangential- and normal components of acceleration.

The position function is

$s(t) = re^{i \theta}$

Differentiating once gives velocity:

$v(t) = \dot{r}e^{i\theta} + i \dot{\theta}re^{i\theta} = (\dot{r} + i\dot{\theta}r)e^{i\theta} $

Differentiating once more gives acceleration, broken down into tangential (real) and normal (imaginary) components as the coefficient of $e^{i\theta}$:

$a(t) = (\ddot{r}+i[\ddot{\theta}r + \dot{r}\dot{\theta}])e^{i\theta} + i\dot{\theta}(\dot{r} +i\dot{\theta}r)e^{i\theta} = ([\ddot{r} - \dot{\theta}^2 r] + i [\ddot{\theta}r + 2\dot{r}\dot{\theta}]) e^{i\theta} $

So much easier than the mental gymnastics needed to derive in $\mathbb{R}^2$

Answer 12

De Moivre's formula can be used (with geometric series) to compute many identities like $$\sum_{k=0}^{n-1}\sin(k\cdot\theta) = \Im\left(\frac{\cos(n\cdot\theta)+i\sin(n\cdot\theta) - 1}{\cos(\theta)+i\sin(\theta)-1}\right)$$ etc. I remember using this one in geometry when proving that the sum of the squares of all the diagonals and sides of a regular n-sided polygon inscribed in the unit circle equals to $n^2$.

The reason why I like this example is because it's not something cool about imaginary themselves, like complex functions or roots; they're certainly cool, but to make use of them one needs to learn much more maths. To understand complex roots, Euler's formula or uses in physics the students need to know what those are; but telling a student who's just learned about Euler's formula is meaningless, as he won't understand what an imagenary exponent means. He'll be confused rather then thrilled.

This example does little more then allowing a matematician to compute a series - but a student who knows about the sine function will understand exactly how it is useful. Unlike factorization etc. I also know of no trivial way to do this without complex numbers.

Answer 13

The identity $$ 4\arctan\left(\frac15\right)-\arctan\left(\frac1{239}\right)=\frac{\pi}4 $$ to calculate $\pi$ using Leibniz's series can easily be proved using complex numbers.

Answer 14

Most integrals that cannot be solved with real methods can be solved with complex contours.

For example, the integral $$\int_{-\infty}^{\infty}\dfrac{1}{(x^2+1)^2}dx=\frac\pi 2$$ by using contour integration.

Answer 15

In my point of view complex analysis is just cool stuff, but perhaps that is somewhat broad. If he knows some analysis: If a complex function is (complex-) differentiable once, it is differentiable infinitely many times! This blew my mind. Or if you know a complex differentiable function on the boundary of a certain area, you can calculate any point of that area with that knowledge!)

I like how you can visually multiply numbers just by adding their angles and multiplying their 'length'. This way it is also easy to find n-th roots graphically.

Now something very cool is that $i^i$ is a real number! (You can easily prove it by using Eulers identity $e^{i\pi} +1 =0$)

EDIT: As @MarcvanLeeuwen pointed out, it does not have a well defined value, there are many possible values:

We know that $e^{i\pi/2} = i$. Therfore $i^i = (e^{i\pi/2})^i = e^{i^2 \pi/2} = e^{-\pi/2} \in \mathbb R$.

But if you add any multiple of $2\pi i$ to the exponent, you will still end up in the same value, since $e^{2\pi i} = 1$, so we are basically 'multiplying by 1'. Therefore for every integer $k$ we can argue that

$e^{i\pi/2} \underbrace{e^{2\pi i k}}_1 = i$ and so

$$(e^{i\pi/2} e^{2\pi i k})^i = (e^{i(\pi/2+2\pi k)})^i = e^{i^2(\pi/2+2\pi k)} = e^{-(\pi/2+2\pi k)} \in \mathbb R$$

Answer 16

Complex numbers are extremely useful in physics, but that may require some more preparation than high school math provides.

The complex numbers though are cool for many reasons. For one, it's cool to be able to solve $x^2=-1$, which if you only know of the reals, then you are probably indoctrinated to think no such solution can meaningfully exist. Another cool thing is the formula $e^{i\pi }=-1$, which can be obtained quite easily by considering series, and taking some facts on faith.

Another cool fact about the complex numbers is that they are algebraically closed, i.e., every polynomial equation has a solution, and in fact, at most $n$ solution, with $n$ the degree of the polynomial. That is really elegant and very elementary proofs exist.

The geometric meaning of addition and multiplication for complex numbers is cool as well, and being able to compute geometrically, e.g., finding all solutions to $z^n=w$, is cool. Moreover, these solutions form a regular $n$-gon, which is cool too.

The fact that all analytic functions of the reals, e.g., $\sin$ etc., can be extended uniquely to an analytical function on the complex numbers is cool, but not very elementary. There are many other cool things, probably almost an endless list...

Answer 17

If you look at the progression of number systems, each step was taken because of operations that exposed a fundamental incompleteness in the number system, eg negative numbers were introduced to compensate for incompleteness of the natural numbers under subtraction, rational numbers compensate for lack of divisibility of any integer by another...

Complex numbers were introduced because of incompleteness of the real numbers under algebraic operations. This take some sophistication to understand, just like it takes some sophistication to understand why negative numbers are useful (it's possible to get around with only positive numbers for quite a while, but it gets cumbersome, cf Diophantus).

Answer 18

Complex numbers are very useful for 2D geometric operations. You can rotate a point by multiplying, move it around by addition and subtraction.

It gets really interesting when you can do things like project a line segment onto another one by dividing..

Answer 19

I'm somewhat surprised that nobody before me has mentioned them, but Gaussian Integers are somewhat cool. They're basically just like the integers, but in 2D, complete with prime factoring. And this leads to the map of Gaussian primes, some of which are viewable here:

You can then show the way that the same properties of rationals, etc, can be extrapolated to apply to the Gaussian equivalent.

Similarly, discussions of other extensions of number systems can be very interesting. For instance, defining $\omega^2=-(\omega+1)$, producing the Eisenstein Integers.

In a similar vein, there is also use of complex numbers to define real curves, like $|z-z_0|=r$ defining a circle with radius $r$ and centre $(x_0,y_0)$, where $z_0=x_0+iy_0$, or $|z-z_1|+|z-z_2|=c$ for an ellipse, etc. In short, the 2D nature of complex numbers can make for interesting tweaks to basic mathematics.

Unfortunately, you're not likely to find anything in complex numbers "cool" enough to capture the interest of non-mathematically-minded students, except maybe things like the Mandelbrot set, mentioned in a previous answer. But these 2D traits of complex numbers are certainly useful.

Answer 20

(Expanding my comment into an answer. Complex roots, integrals, and trig identities are preaching to the choir. If you consider those things "cool", then you probably think the same about the concept of complex numbers themselves, and therefore do not need any convincing. Contrapositively, people who do not yet see the intrinsic beauty of the complex plane are unlikely to be persuaded by other examples of abstract math.)

Here's a weird name that most students have never heard of: Quadrature Phase Shift Keying (QPSK). It's a way to convert data into a signal that can be transmitted on radio waves. Many important technologies use QPSK or its siblings:

• Direct Sequence Spread Spectrum (DSSS)
• Orthogonal Frequency Division Multiplexing (OFDM)
• Quadrature Amplitude Modulation (QAM)

Huh, you haven't heard of those either? Okay, what about these names:

• WiFi, which uses DSSS
• 3G and 4G, which use OFDM
• HDTV, which uses QAM

Show of hands, how many of you use a laptop, or a tablet, or a smartphone, or a TV? I see hands from 1, 2, 3, ... everyone in the room. Congratulations, you are relying on complex numbers.

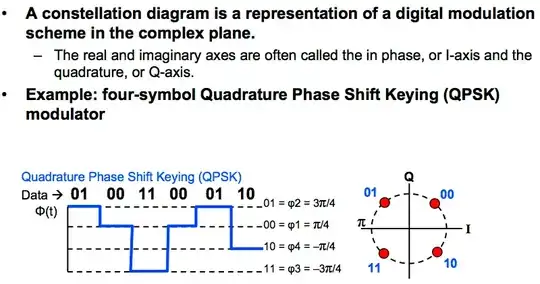
QPSK takes two bits of data and uses a table to convert it into a complex number, which is then transmitted as a phase shift (from Euler's formula $e^{i\theta} = \cos \theta + i \sin \theta$). Sending two bits isn't much, but when a radio chip does that over and over, millions of times per second, it adds up to a lot of useful stuff: email, videos, apps, cat gifs, etc. At the receiving end, a chip does it all in reverse, converting the radio wave into complex numbers, and from there back to the original data.

This rigamarole is necessary to make the signals better at handling interference. It's how so many people can use WiFi or 4G or whatever at the same time, without the signals drowning each other out. Imagine you're with a hundred people standing in the gym, holding 50 different conversations, but the person you're talking to is on the other side of the room. Complex numbers are part of the process that lets your device pick out the tiny handful of radio waves that it needs from the huge mass of noise.

Answer 21

Since it does not appear that Fractals are mentioned, I would mention those. The pictures on wikipedia are absolutely gorgeous: http://en.wikipedia.org/wiki/Mandelbrot_set

Fractals such as the Mandelbrot set are built using the boundedness of an iterative complex function. The explanation of how the set takes on its shape is beyond me as a mechanical engineer, but it is certainly cool to look at. Also, it's one that you can write a simple program and let the students vary the exponentiation parameter and see how the shape changes.

EDIT: Didn't see the bit so much about practical.

In that event, I would recommend talking to their physics teacher about showing RL/RC/RLC circuits. The impedance of those circuits is based on complex numbers, and can be used in physics class as well. If your school physics lab has oscilloscopes, they can graphically see magnitude/phase of input signal (a sine wave) vs the output signal for a 2nd-order (RLC) circuit. The input is a square wave for the 1st order (RC/RL) circuits. If you want some synthesized pictures/explanation of the circuit theory, I can write that up.

Answer 22

Complex numbers can be though of as an algebraic modelisation of groups of geometrical transformations: every direct similarity of the plane can be represented by a function: \begin{align*} f: &\mathbb{C}\rightarrow \mathbb{C} \\ &z\mapsto az+b \end{align*} for some $a,b\in\mathbb{C}$.

This allows to calculate the centers of composed similarities, argument and module of complex numbers have geometrical sense...

Answer 23

Even though I have only a single line of hearsay as an application of such, the derivation of primitive/all Pythagorean triples via complex factorisation (see here or here; they might not look brief but really are) always did strike me as both natural and really neat. Can't factor a sum of squares? Surprise, it's a difference after all!

Answer 24

Complex numbers can be used to give a very simple and short proof that the sum of the angles of a triangle is 180 degrees. Construct a triangle in the plane whose vertices are complex numbers z1.z2 and z3 in the plane.

Recall that the angle $\theta$ at a vertex like $ABC$ is the angular part $\theta$ of $(C-B)/(A-B) = r\exp(i\theta)$. It is written $\theta = \arg(r\exp(i\theta))$ and is defined only modulo $2\pi$, although conventionally a representative in the interval $(-\pi, \pi]$ is taken.

Now recall that $\arg(z w) =\arg(z) + \arg(w)$ for any nonzero complex numbers $z$ and $w$: this follows immediately from the multiplicative property of the exponential, $\exp(i\theta)\exp(i\phi) = \exp(i(\theta + \phi))$.

The sum of the three angles at vertices $Z1$, $Z2$, and $Z3$ is obtained merely by rearranging the product of three numbers in the denominator of a fraction. So now:

$$\eqalign{\arg\frac{Z2-Z1}{Z3-Z1} + \arg\frac{Z3-Z2}{Z1-Z2}+\arg\frac{Z1-Z3}{Z2-Z3} &= \arg\left(\frac{Z2-Z1}{Z3-Z1}\frac{Z1-Z3}{Z2-Z3}\right) \\ &= \arg\left(\frac{Z2-Z1}{Z1-Z2}\frac{Z3-Z2}{Z2-Z3}\frac{Z1-Z3}{Z3-Z1}\right) \\ &= \arg\left(-1^3\right) = \arg(-1) \\ &= \pi. }$$

Ligget se. I'll always remember Ravi Kulkarni showing us this trick at the end of one of his lectures and quoting his granddaughter, "Cool." I hope your students agree-especially if they've just been tortured with the painfully tedious classical proof of the result.

Answer 25

By far the coolest thing about complex numbers is that nature embraces them.

Throw a die. Since Newton we know how non-linear dynamics laws are supposed to govern the probabilistic outcomes. Now we know better. We understand nature at a more fundamental level. And at that level we work with complex amplitudes, the 2-norm of which corresponds to observed probabilities. The truly amazing thing is that the dynamics laws that govern the complex amplitude dynamics are entirely linear.

That's right, all the complexity and chaotic behavior observed in real life, exemplified by the throw of a die, results from fundamentally simple linear evolution laws. And for these laws to work and to produce the richness of behaviors we observe, you have to introduce a complex number description of nature.

Complex numbers are a necessity. Without them, you can't understand the physical world.