Related: Visually stunning math concepts which are easy to explain
Beside the wonderful examples above, there should also be counterexamples, where visually intuitive demonstrations are actually wrong. (e.g. missing square puzzle)
Do you know the other examples?
The never ending chocolate bar!
If only I knew of this as a child..
The trick here is that the left piece that is three bars wide grows at the bottom when it slides up. In reality, what would happen is that there would be a gap at the right between the three-bar piece and the cut. This gap is is three bars wide and one-third of a bar tall, explaining how we ended up with an "extra" piece.
Side by side comparison:
Notice how the base of the three-wide bar grows. Here's what it would look like in reality$^1$:
1: Picture source https://www.youtube.com/watch?v=Zx7vUP6f3GM
Visualization can be misleading when working with alternating series. A classical example is \begin{align*} \ln 2=&\frac11-\frac12+\frac13-\frac14+\;\frac15-\;\frac16\;+\ldots,\\ \frac{\ln 2}{2}=&\frac12-\frac14+\frac16-\frac18+\frac1{10}-\frac1{12}+\ldots \end{align*} Adding the two series, one finds \begin{align*}\frac32\ln 2=&\left(\frac11+\frac13+\frac15+\ldots\right)-2\left(\frac14+\frac18+\frac1{12}+\ldots\right)=\\ =&\frac11-\frac12+\frac13-\frac14+\;\frac15-\;\frac16\;+\ldots=\\ =&\ln2. \end{align*}
Here's how to trick students new to calculus (applicable only if they don't have graphing calculators, at that time):
$0$. Ask them to find inverse of $x+\sin(x)$, which they will unable to. Then,
$1$. Ask them to draw graph of $x+\sin(x)$.
$2$. Ask them to draw graph of $x-\sin(x)$
$3$. Ask them to draw $y=x$ on both graphs.
Here's what they will do :
$4$. Ask them, "What do you conclude?". They will say that they are inverses of each other. And then get very confused.
Construct a rectangle $ABCD$. Now identify a point $E$ such that $CD = CE$ and the angle $\angle DCE$ is a non-zero angle. Take the perpendicular bisector of $AD$, crossing at $F$, and the perpendicular bisector of $AE$, crossing at $G$. Label where the two perpendicular bisectors intersect as $H$ and join this point to $A$, $B$, $C$, $D$, and $E$.
Now, $AH=DH$ because $FH$ is a perpendicular bisector; similarly $BH = CH$. $AH=EH$ because $GH$ is a perpendicular bisector, so $DH = EH$. And by construction $BA = CD = CE$. So the triangles $ABH$, $DCH$ and $ECH$ are congruent, and so the angles $\angle ABH$, $\angle DCH$ and $\angle ECH$ are equal.
But if the angles $\angle DCH$ and $\angle ECH$ are equal then the angle $\angle DCE$ must be zero, which is a contradiction.
Proof : Let $O$ be the intersection of the bisector $[BC]$ and the bisector of $\widehat{BAC}$. Then $OB=OC$ and $\widehat{BAO}=\widehat{CAO}$. So the triangles $BOA$ and $COA$ are the same and $BA=CA$.
A favorite of mine was always the following:
\begin{align*} \require{cancel}\frac{64}{16} = \frac{\cancel{6}4}{1\cancel{6}} = 4 \end{align*}
I particularly like this one because of how simple it is and how it gets the right answer, though for the wrong reasons of course.
Another example :
From "Pastiches, paradoxes, sophismes, etc." and solution page 23 : http://www.scribd.com/JJacquelin/documents
A copy of the solution is added below. The translation of the comment is :
Explanation : The points A, B and P are not on a straight line ( the Area of the triangle ABP is 0.5 ) The graphical highlight is magnified only on the left side of the figure.
I think this could be the goats puzzle (Monty Hall problem) which is nicely visually represented with simple doors.
Three doors, behind 2 are goats, behind 1 is a prize.
You choose a door to open to try and get the prize, but before you open it, one of the other doors is opened to reveal a goat. You then have the option of changing your mind. Should you change your decision?
From looking at the diagram above, you know for a fact that you have a 1/3rd chance of guessing correctly.
Next, a door with a goat in is opened:
A cursory glance suggests that your odds have improved from 1/3rd to a 50/50 chance of getting it right. But the truth is different...
By calculating all possibilities we see that if you change, you have a higher chance of winning.
The easiest way to think about it for me is, if you choose the car first, switching is guaranteed to be a goat. If you choose a goat first, switching is guaranteed to be a car. You're more likely to choose a goat first because there are more goats, so you should always switch.
A recent example I found which is credited to Martin Gardner and is similar to some of the others posted here but perhaps with a slightly different reason for being wrong, as the diagonal cut really is straight.
I found the image at a blog belonging to Greg Ross.
Spoilers
The triangles being cut out are not isosceles as you might think but really have base $1$ and height $1.1$ (as they are clearly similar to the larger triangles). This means that the resulting rectangle is really $11\times 9.9$ and not the reported $11\times 10$.
Squaring the circle with Kochanski's Approximation1
1: http://mathworld.wolfram.com/KochanskisApproximation.html
That $\sum_{n=1}^\infty n = -\frac{1}{12}$. http://www.numberphile.com/videos/analytical_continuation1.html
The way it is presented in the clip is completely incorrect, and could spark a great discussion as to why.
Some students may notice the hand-waving 'let's intuitively accept $1 -1 +1 -1 ... = 0.5$.
If we accept this assumption (and the operations on divergent sums that are usually not allowed) we can get to the result.
A discussion that the seemingly nonsense result directly follows a nonsense assumption is useful. This can reinforce why it's important to distinguish between convergent and divergent series. This can be done within the framework of convergent series.
A deeper discussion can consider the implications of allowing such a definition for divergent sequences - ie Ramanujan summation - and can lead to a discussion on whether such a definition is useful given it leads to seemingly nonsense results. I find this is interesting to open up the ideas that mathematics is not set in stone and can link to the history of irrational and imaginary numbers (which historically have been considered less-than-rigorous or interesting-but-not-useful).
\begin{equation} \log6=\log(1+2+3)=\log 1+\log 2+\log 3 \end{equation}
I might be a bit late to the party, but here is one which my maths teacher has shown to me, which I find to be a very nice example why one shouldn't solve an equation by looking at the hand-drawn plots, or even computer-generated ones.
Consider the following equation: $$\left(\frac{1}{16}\right)^x=\log_{\frac{1}{16}}x$$
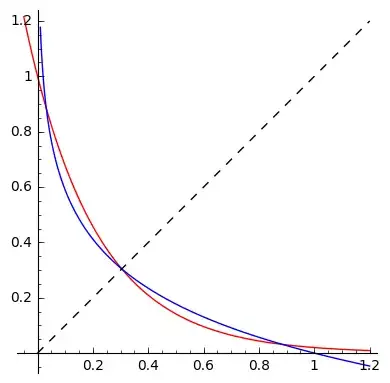
At least where I live, it is taught in school how the exponential and logarithmic plots look like when base is between $0$ and $1$, so a student should be able to draw a plot which would look like this:
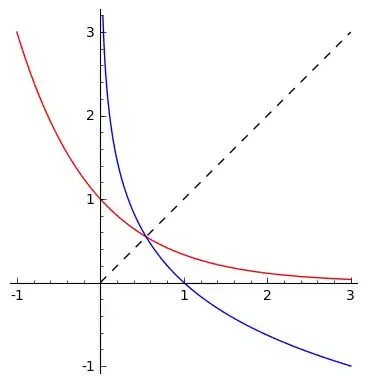
Easy, right? Clearly there is just one solution, lying at the intersection of the graphs with the $x=y$ line (the dashed one; note the plots are each other's reflections in that line).
Well, this is clear at least until you try some simple values of $x$. Namely, plugging in $x=\frac{1}{2}$ or $\frac{1}{4}$ gives you two more solutions! So what's going on?
In fact, I have intentionally put in an incorrect plots (you get the picture above if you replace $16$ by $3$). The real plot looks like this:
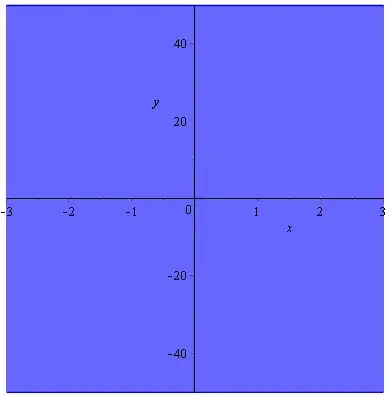
You might disagree, but to be it still seems like it's a plot with just one intersection point. But, in fact, the part where the two plots meet has all three points of intersection. Zooming in on the interval with all the solutions lets one barely see what's going on:
The oscillations are truly minuscule there. Here is the plot of the difference of the two functions on this interval:
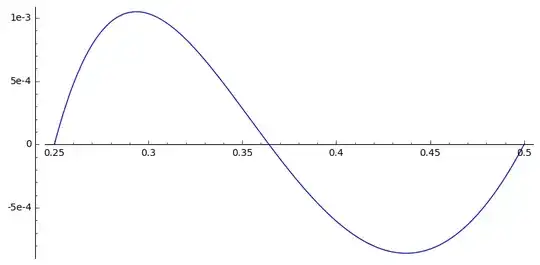
Note the scale of the $y$ axis: the differences are on the order of $10^{-3}$. Good luck drawing that by hand!
To get a better idea of what's going on with the plots, here they are with $16$ replaced by $50$:
One of my favorites:
\begin{align} x&=y\\ x^2&=xy\\ x^2-y^2&=xy-y^2\\ \frac{(x^2-y^2)}{(x-y)}&=\frac{(xy-y^2)}{(x-y)}\\ x+y&=y\\ \end{align}
Therefore, $1+1=1$
The error here is in dividing by x-y
Here is one I saw on a whiteboard as a kid... \begin{align*} 1=\sqrt{1}=\sqrt{-1\times-1}=\sqrt{-1}\times\sqrt{-1}=\sqrt{-1}^2=-1 \end{align*}
There are two examples on Wikipedia:Missing_square_puzzle Sam Loyd's paradoxical dissection, and Mitsunobu Matsuyama's "Paradox". But I cannot think of something that is not a dissection.
Here is a measure theoretic one. By 'Picture', if we take a cover of $A:=[0,1]∩\mathbb{Q}$ by open intervals, we have an interval around every rational and so we also cover $[0,1]$; the Lebesgue measure of [0,1] is 1, so the measure of $A$ is 1. As a sanity check, the complement of this cover in $[0,1]$ can't contain any intervals, so its measure is surely negligible.
This is of course wrong, as the set of all rationals has Lebesgue measure $0$, and sets with no intervals need not have measure 0: see the fat Cantor set. In addition, if you fix the 'diagonal enumeration' of the rationals and take $\varepsilon$ small enough, the complement of the cover in $[0,1]$ contains $2^{ℵ_0}$ irrationals. I recently learned this from this MSE post.
This is essentially the same as the chocolate-puzzle. It's easier to see, however, that the total square shrinks.
To give a contrarian interpretation of the question I will chime in with Goldbach's comet which counts the number of ways an integer can be expressed as the sum of two primes:
It is mathematically "wrong" because there is no proof that this function doesn't equal zero infitely often, and it is visually deceptive because it appears to be unbounded with its lower bound increasing at a linear rate.
This is my favorite.
\begin{align}-20 &= -20\\ 16 - 16 - 20 &= 25 - 25 - 20\\ 16 - 36 &= 25 - 45\\ 16 - 36 + \frac{81}{4} &= 25 - 45 + \frac{81}{4}\\ \left(4 - \frac{9}{2}\right)^2 &= \left(5 - \frac{9}{2}\right)^2\\ 4 - \frac{9}{2} &= 5 - \frac{9}{2}\\ 4 &= 5 \end{align}
You can generalize it to get any $a=b$ that you'd like this way:
\begin{align}-ab&=-ab\\ a^2 - a^2 - ab &= b^2 - b^2 - ab\\ a^2 - a(a + b) &= b^2 -b(a+b)\\ a^2 - a(a + b) + \frac{a + b}{2} &= b^2 -b(a+b) + \frac{a + b}{2}\\ \left(a - \frac{a+b}{2}\right)^2 &= \left(b - \frac{a+b}{2}\right)^2\\ a - \frac{a+b}{2} &= b - \frac{a+b}{2}\\ a &= b\\ \end{align}
It's beautiful because visually the "error" is obvious in the line $\left(4 - \frac{9}{2}\right)^2 = \left(5 - \frac{9}{2}\right)^2$, leading the observer to investigate the reverse FOIL process from the step before, even though this line is valid. I think part of the problem also stems from the fact that grade school / high school math education for the average person teaches there's only one "right" way to work problems and you always simplify, so most people are already confused by the un-simplifying process leading up to this point.
I've found that the number of people who can find the error unaided is something less than 1 in 4. Disappointingly, I've had several people tell me the problem stems from the fact that I started with negative numbers. :-(
Solution
When working with variables, people often remember that $c^2 = d^2 \implies c = \pm d$, but forget that when working with concrete values because the tendency to simplify everything leads them to turn squares of negatives into squares of positives before applying the square root. The number of people that I've shown this to who can find the error is a small sample size, but I've found some people can carefully evaluate each line and find the error, and then can't explain it even after they've correctly evaluated $\left(-\frac{1}{2}\right)^2=\left(\frac{1}{2}\right)^2$.
This is a fake visual proof that a sphere has Euclidean geometry.
My favourite is: Is the area of both shapes are equal?
It looks like
$$area=\frac{44×86}2=22×86$$
But, the triangle is impossible!
I don't know about you but to me, it looks like the hexagons are stretched horizontally. If you also see it that way and you trust your eyes, then you could take that as a visual proof that $\tan\frac{7}{4} < 60^\circ$. If that's how you saw it, then it's an optical illusion because the hexagons are really stretched vertically. Unlike some optical illusions of images that appear different than they are but are still mathematically possible, this is an optical illusion of a mathematically impossible image. The math shows that $\tan^{-1} 60^\circ = \sqrt{3}$ and $\sqrt{3} < \frac{7}{4}$ because $7^2 = 49$ but $3 \times 4^2$ = 48. It's just like it's mathematically impossible for something to not be moving when it is moving but it's theoretically possible for your eyes to stop sending movement signals to your brain and have you not see movement in something that is moving which would look creepy for those who have not experienced it because your brain could still tell by a more complex method than signals from the eyes that it actually is moving.
To draw a hexagonal grid over a square grid more accurately, only the math and not your eye signals can be trusted to help you do it accurately. The math shows that the continued fraction of $\sqrt{3}$ is [1; 1, 2, 1, 2, 1, 2, 1 ... which is less than $\frac{7}{4}$, not more.
I do not think this really qualify as "visually intuitive", but it is definitely funny
http://www.youtube.com/watch?v=YoHxuHEGFGQ
They do such a great job at dramatizing these kind of situations. Who cannot remember of an instance in which he has been either a "Billy" or a "Pa' and Ma'"? Maybe more "Pa' and Ma'" instances on my part...;)
