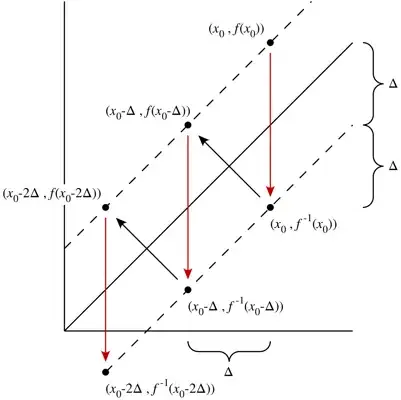
In the formulation of the question the function $f$ is one-to-one and onto. Below two proofs are presented. The first one requires the one-to-one and assumption, while the second one does not.
First answer requiring that $f$ is one-to-one.
Clearly, $f$ is also onto, as an arbitrary $x\in[0,1]$, is the image of $2x-f(x)$, and since
$f$ is one-to-one and onto, $f$ possesses an inverse $f^{-1}:[0,1]\to [0,1]$.
The functional relation $f\big(2x-f(x)\big)=x$, implies
$$
f(x)-x=x-f^{-1}(x). \tag{1}
$$
We shall show that $f(x)=x$. Assume not. Then
$$
f(x_0)-x_0\ne 0,
$$
for some $x_0\in(0,1)$. Let's assume that $f(x_0)-x_0=a>0$. Then $(1)$ implies that
$$
f(x_0)-x_0=x_0-f^{-1}(x_0)=f^{-1}(x_0)-f^{-2}(x_0)=\cdots=f^{-k}(x_0)-f^{-(k+1)}(x_0),
$$
for every $k\in\mathbb N$, where $f^{-k}$ is $f^{-1}\circ\cdots\circ f^{-1}$ $k$ times.
But this means that
$$
f^{-1}(x_0)=x_0-a,\,\,f^{-2}(x_0)=x_0-2a,\ldots,f^{-k}(x_0)=x_0-ka,
$$
which means that $\lim_{k\to\infty}f^{-k}(x_0)=-\infty$. A contradiction,
$f^{-k}(x_0)\in [0,1]$.
We would reach to a contradiction even if we had assumed that $a<0$.
Second answer not requiring that $f$ is one-to-one.
As $f\big(2x - f(x)\big) = x,\,$ for all $x \in \left[ {0,1} \right]$, then
$$
0 \le 2x - f(x) \le 1 \quad \Longrightarrow\quad 2x - 1 \le f(x) \le 2x,\,\,\,
\text{for all $x \in \left[ {0,1} \right]$.}
$$
Replacing in the above $x$ with $2x - f(x)$ we obtain
\begin{align}
2\big( {2x - f(x)} \big) - 1 \le f\big( {2x - f(x)} \big) \le 2\big( {2x - f(x)} \big),
\end{align}
or
\begin{align}
2\big( {2x - f(x)} \big) - 1 \le x \le 2\big( {2x - f(x)} \big)
\end{align}
which implies that
$$
\frac{3x-1}{2}\le f(x) \le \frac{3x}{2}.
$$
Repetition of this process produces the following inequalities
$$
x+\frac{x-1}{n}\le f(x)\le x+\frac{x}{n},\,\,\,
\text{for all $x \in \left[ {0,1} \right]\,\,$ and $\,\,n\in\mathbb N$,}
$$
and therefore
$$
f(x)=x ,\,\,\,
\text{for all $x \in \left[ {0,1} \right]$.}
$$