68

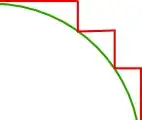
The infamous "$\pi = 4$" proof was already discussed here:

Is value of $\pi = 4$?

And I have read all the answers, yet I think that they will not be of much help to me if I try to explain this thing to a non mathematician. The main missing point, in my opinion, is the fact that length of curves is defined using polygonal approximations (discrete approximation of the curve obtained by taking the straight-lines connecting a finite sequence of points on the curve).

However, a layman would ask "why is your strange 'polygonal approximation' method correct, but the $\pi = 4$ proof's method incorrect?" and I have to admit I fail to see strong arguments to convince him here.

So my question might be better stated as "convince a layman the correct way to measure lengths of curves is our (the mathematician's) way"; however, I'm interested specifically in the $\pi = 4$ proof and will be glad to hear totally different approaches to it.

Alex Ortiz
  • 18,901
  • 2
  • 29
  • 69
Gadi A
  • 18,225
  • 6
  • 73
  • 116
  • 27
    I would actually try to topple their intuition with Koch's snowflake. After that they will understand how much they don't understand, well usually. – Asaf Karagila Jun 04 '11 at 04:48
  • This is actually a very good idea for the final chord in a post about this matter. Thanks! – Gadi A Jun 04 '11 at 04:56
  • 3
    Well if they think that this method works then it should also work for a circle in a triangle, and a circle in a hexagon, but then in that case the same method produces a different answer... – N. S. Jun 04 '11 at 05:02
  • 3
    To convince them that using pi is the right way to measure: Nothing convinces the layman like a physical measurement. – trutheality Jun 04 '11 at 07:17
  • @Asaf [Hypnotic...](http://upload.wikimedia.org/wikipedia/commons/6/65/Kochsim.gif) – Mateen Ulhaq Jun 05 '11 at 05:08
  • 2
    Would it be correct to think that since the number of corners increases to infinity, there will be infinite number of infinitely small differences? Thus the problem is reduced to convincing indeterminateness of indeterminate forms, which is kind of easier to explain. – Cloudanger Feb 16 '12 at 01:45
  • 1
    I note that the title question would make this essentially a duplicate of the question linked to (explain what is wrong with the bogus proof), but that the body text tries to transform it into a different, harder, question. I would paraphrase that as "how can one explain that _in spite of the fact that naive application can lead to wrong answers_ we can use approximation by polygonal lines to define/compute the length of curves". It is never a good idea to make title and body questions diverge. Very disappointingly **nobody** seems to have answered the more interesting body question, to date – Marc van Leeuwen Aug 14 '13 at 07:28
  • 5
    "A layman would ask 'why is your strange 'polygonal approximation' method correct, but the π=4 proof's method incorrect?' and I have to admit I fail to see strong arguments to convince him here." The π=4 method isn't "incorrect", it just gives a different notion of distance than Euclidean distance. In fact, the distance it gives is perfectly valid: it's the taxicab metric perimeter of the circle. It's a perfectly reasonable notion of distance, it just isn't the Euclidean distance we talk about in every day life: the one that is invariant under rigid rotations/translations, etc. – Marcel Besixdouze Mar 15 '16 at 21:55
  • first you need to find a layman that beleives that "proof" – Jasen Jul 07 '16 at 03:38
  • Someone has changed the "layman" in the title to the supposedly gender-neutral "layperson". i wonder if someday I have to call myself a "huperson". – user1551 Mar 06 '18 at 20:45

15 Answers15

78

Use a similar "zig-zag" approach to "show" that the diagonal of a $100$ meter by $100$ meter field is $200$. Everybody who has ever crossed a field will know that walking $1$ meter north, then $1$ meter east, then $1$ north, then $1$ east, and so on is a lousy way to do it.

André Nicolas
  • 491,093
  • 43
  • 517
  • 948
  • 14
    Of course, they could still ask why *this* proof is wrong. Or is it only mathematicians who want to know *why* a proof is wrong even when they know it is? – ShreevatsaR Jun 04 '11 at 04:40
  • 5
    This is mathematically the same as the analogy Ross Millikan gave at the other question, but I like the very concrete description. I think it is easier to see what is intuitively wrong with the diagonal problem because it is scale invariant; you are locally overestimating the length by the same factor as if you just walked along the edge of the field. If someone doesn't at first buy that this logic transfers to circles, perhaps they can be convinced intuitively that if you zoom in enough on a circle it looks like a straight line, and locally you're badly estimating diagonals of rectangles. – Jonas Meyer Jun 04 '11 at 04:53
  • 5
    @ShreevatsaR: I think that to the "layman" there is no useful distinction between **that** it is wrong and **why** it is wrong. The answer would have been different if one was dealing with a first-year calculus student, though the concrete field example should still be a part of the explanation. – André Nicolas Jun 04 '11 at 05:03
  • 2
    @Jonas Meyer: The scale-invariance comment could be turned into a useful visual aid. For the circle, halve the length of the zigs, then enlarge the picture by a factor of $2$. Do something similar with the usual polygonal approximation. There is a dramatic visual difference. – André Nicolas Jun 04 '11 at 05:10
67

I think the problem is that that there is a mix-up between perimeter and surface.

By caving in the corners, the diagram gets people's attention on the apparent similarity in surface of the erstwhile square and forget that what matters is the perimeter.

Close up

Show him this picture and ask him which line is longer. Then ask him if breaking the red line with even more corners would make it shorter.

Once he realize that it is the length of the line that matters and not the area, the argument should be understood.

Sylverdrag
  • 1,474
  • 1
  • 11
  • 11
  • 3
    Good point about surface vs circumference. The approach is only good for the first. – gjvdkamp Aug 30 '11 at 12:05
  • 3
    Sorry to be dense, but could someone tell me what "surface" means in this context? The only definition of "surface" that I know is "2-manifold." Is "surface" supposed to be a synonym for "area"? – Jesse Madnick Nov 18 '13 at 00:27
  • 1
    @JesseMadnick Usually, when the only definition you know does not match the context, the logical next step is to look up the word in a dictionary. According to the American Heritage dictionary, one of the definitions for the word "surface" is: [Mathematics] "A portion of space having length and breadth but no thickness." Does that help? – Sylverdrag Nov 18 '13 at 06:10
  • 7
    Yes, thank you. I could have done with less condescension, but yes, it helps. – Jesse Madnick Nov 18 '13 at 06:19
  • 1
    That's probably because I read your your original comment to my 2 years old answer as a critique rather than as a genuine question. – Sylverdrag Nov 18 '13 at 07:53
17

Tell your layman about the difference between the euclidean metric and the "taxicab metric". The euclidean length of a segment $\Delta {\bf z}=(\Delta x, \Delta y)$ is $\sqrt{\Delta x^2 + \Delta y^2}$ whereas the "taxicab" length of this segment is $|\Delta x|+|\Delta y|$. "In the limit" this implies that the euclidean circumference of the unit circle is $2\pi$, whereas the "taxicab circumference" is $4$.

Christian Blatter
  • 216,873
  • 13
  • 166
  • 425
  • 1
    Further reading: [Euclidean distance](http://en.wikipedia.org/wiki/Euclidean_distance) and [taxicab distance](http://en.wikipedia.org/wiki/Taxicab_distance). – Rory O'Kane Nov 13 '12 at 08:46
12

Disclaimer This is not a rigorous approach, at all, since the question is not framed as it was in the similar, earlier, linked question. I'm trying to provide an appeal to intuition that helps to "get one's foot in the door" when trying to convince a laywoman that it is faulty. Once such an individual comes to doubt the faulty proof, he/she will be better prepared, and open to, a more rigorous explanation/proof that the circumference of said circle is, indeed, $\pi$

In trying to keep to the "perimeter of square = circumference of circle inscribed in the square" conjecture, but in keeping with user6312's suggestion: for those who believe the "proof" you linked to, and even those who aren't sure what to believe...

Ask them if they were in a race, and had the choice of whether to run on one of two tracks: 1. a square track of perimeter 400 meters, or 2. a circular track that is "inside" the square, touching the square only at the midpoints of the square's edges, which track would they choose?

Most, I suspect, would opt, rather immediately, to choose running on the circular track . Upon their response, ask them "Why? - then show the connection to the "proof that $\pi = 4$", and "run" through the mathematical approach to arriving at the circumference of a circle (no pun intended!).

Alternatively, you could ask them to bet on a race where two world-class top-seeded sprinters were racing against one another, with Runner1 randomly selected to run the race on the "square track", and Runner2 to run on the "circular track." On whom would they bet, and why? Again, you'll have your "foot in the door" to challenging the "$\pi = 4$" claim.

Just a thought...

amWhy
  • 204,278
  • 154
  • 264
  • 488
12

Notice that in this argument $\pi$ ends up equalling 4 since that is the perimeter of the circumscribing square. Taking a square is completely arbitrary though, just show your layman the same argument starting with a triangle or pentagon or even something like this:

some random irregular polyhedron

Then after showing about 3 separate cases all ending up with the circumference of the starting figure instead of $\pi$, I'd say even the least mathematically inclined should get the invalidity of the argument.

gfes
  • 726
  • 3
  • 7
9

The way I like to think of it is that while the length contained in each peak DOES decrease, there are more peaks each time, so the total length stays the same. Or more colloquially, it gets (infinitely) fuzzy but it never gets smooth.

El'endia Starman
  • 3,918
  • 24
  • 41
  • The fuzzy/smooth imagery is really cool; thanks for sharing that. Have you had any success explaining this to others? – Eric Stucky May 30 '12 at 00:02
  • @EricStucky: A little bit. It's been almost a year since I had to though... – El'endia Starman May 30 '12 at 00:31
  • 3
    This explanation is actually simply incorrect. In any reasonable way, the sequence of curves absolutely do converge to the circle. It just so happens that the limit involved in calculating the perimeter does not commute with the limit of the curves. There are theorems which give sufficient conditions for these limits to commute, and you are correct this sequence violates any of those conditions: but violating the condition of an implication does not guarantee the conclusion fails. Your reasoning is backwards. I imagine you are confusing this example with something like the Koch snowflake. – Marcel Besixdouze Mar 15 '16 at 21:58
5

Recently, I had the occasion to explain this to someone. Here's how I went about it. Lets consider where the case of the diagonal of a unit square seems to be well approximated by the step-like curve. At first sight, it seems convincing simply because as the steps increase the jagged line seems to become like a straight line. But this is simply because we can only see up to a certain resolution. Whatever be the number of steps, if one were to zoom into a part of the figure, we'd see exactly a similar sight as before we zoomed in. This is reflected in the fact that in the limit the length of the step-like curve is still $2$. At, this point the person will say but the enclosed figure seems to look the same. And then you say, Exactly! And the measure of the enclosed planar figure is called Area, which indeed tends to the area of the rectangle (this is the basic intuition behind basic integration).

Added

On hindsight, its better to say that the enclosed figure is the one formed by the steps and the diagonal. And the fact that they look the same means that the measure of the enclosed figure (area) tends to zero.

Dactyl
  • 2,684
  • 18
  • 26
5

If you zig-zag instead of following a straight line, your mileage will be higher than if you'd gone straight. A similar thing happens here.

Michael Hardy
  • 1
  • 30
  • 276
  • 565
4

Show them that if you did a $\pi$ approximation by using the area of the figures that the approximation does approach the actual value of $\pi$. You can then tell them that while the area of the figure is approaching the area of the circle the perimeter doesn't approach the circumference, because of the way that it was cut.

You could then talk about how if you circumscribed regular polygons with an increasing number of sides, that the perimeter WOULD approach the circumference.

I think that would do a pretty decent job.

Tauf
  • 134
  • 2
4

As I understand it, one rigorous resolution to this "paradox" comes about by noting that two limiting processes are involved: measuring length requires a limit process (i.e. finer and finer approximations to the curve by discrete polygons), and the square $\rightarrow$ circle construction also requires taking a limit. Depending on the order in which these limits are taken, you can get either $4$ or $\pi$.

In answer to the following question:

However, a layman would ask "why is your strange 'polygonal approximation' method correct, but the π=4 proof's method incorrect?"

Perhaps one approach might be to show that other intuitive methods of measuring length also give the same conclusions: for example, one method for measuring the perimeter of a shape is to trace its outline in string, and then measure the length of the string. In the case of a real, physical "string", this method is limited in accuracy by maximum curvature that can be attained with the string. If the shape involves too many tight zig-zags then those will be smoothed out leading to an underestimate of the total perimeter. Finding the actual perimeter of the shape involves moving to finer and finer types of string (from thick rope, to cotton twine, to thread, to...), which can be forced into tighter and tighter curves.

In other words, we again have a limit process, but here it involves the maximum curvature of the approximation, rather than the number of segments in a polygon. This leads to exactly the same results: depending on the order in which the limits are taken (i.e. in the curvature of the string, or in the construction of the circle), we get either $4$ or $\pi$.

duncanm
  • 423
  • 3
  • 7
3

The simplest way to convey what is wrong with this "proof" that I can think of is:

  1. As you subdivide the square to closer approximate the circle, repeatedly "to infinity", the zig-zags in the line not only become infinitely small, but at the same time you end up with an infinitely large number of them. You cannot have one effect without the other.

  2. Ask the person "How big is an infinitely large number of infinitely small things?"

Hopefully this will manage to convey the notion that just because something is "infinitely small", doesn't mean it is literally zero, and that an infinitely large number of them doesn't actually tell us anything more about a problem than "the result is multiplied by an unknown number between zero and infinity"

Dan
  • 31
  • 1
2

Non-rigorous proof

Give this one a try - I think the part "the author has convinced you that the shortest distance between two points is not a straight line" bit will be easily understood / accessible, even if the mathematics is not.

Also the "staircase" analogy might help, most people will understand that.

Donavuchi Di Vincenzo
  • 21
  • 1
1

I would explain as follows:

Say to the layman that if you added up the length of all the horizontal lines without the vertical lines then the result would equal the circumference of the circle. I am not saying that this is correct but it would sound correct and logical. It would then be clear (even if still confusing) that adding up all the horizontal and vertical lines will give an incorrect answer. He would intuitively understand that the answer should be less than 4.

Shimon Symonds
  • 11
  • 1
1

Think of it this way: when you use the method given above, the perimeter never approaches that of a circle, for the perimeter is always the same (meaning that you cannot apply the concept of 'approaching' something...all you approach is an infinitesimally small set of zig-zagged lines, and even more mess than you started with :() Now, in contrary, when you apply the same method to calculate the area of the circle and not the perimeter, you definitely do approach something, as you continue the process for infinitely many times -- for the area gets increasingly shorter and shorter -- and the limit is the area of the circle. I understand that it can be argued that there still are many zig-zagged lines when you approach the area, but the point is that it can always be made shorter by continuing the process again by many times, which will give a shorter area each time but never an area smaller than that of the circle, which is the definition of 'approaching' a limit. However, in the case of perimeter, all the processes you do are in vain as you never really approach any value, which is to say that its limit does not exist.

Gaurab Bhandari
  • 11
  • 1
0

pi can be experimentaly proven to differ significantly from 4, eg: use a piece of string and a cylindrical can.

considering this demonstration in the context of the faulty proof should quickly lead to an understanding of flaws of the rectilinear approximation of the circumference.

Jasen
  • 134
  • 4