Probability that a quadratic equation has real roots

Question

Problem

The premise is almost the same as in this question. I'll restate for convenience.

Let $A$, $B$, $C$ be independent random variables uniformly distributed between $(-1,+1)$. What is the probability that the polynomial $Ax^2+Bx+C$ has real roots?

Note: The distribution is now $-1$ to $+1$ instead of $0$ to $1$.

My Attempt

Preparation

When the coefficients are sampled from $\mathcal{U}(0,1)$, the probability for the discriminant to be non-negative that is, $P(B^2-4AC\geq0) \approx 25.4\% $. This value can be obtained theoretically as well as experimentally. The link I shared above to the older question has several good answers discussing both approaches.

Changing the sampling interval to $(-1, +1)$ makes things a bit difficult from the theoretical perspective. Experimentally, it is rather simple. This is the code I wrote to simulate the experiment for $\mathcal{U}(0,1)$. Changing it from (0, theta) to (-1, +1) gives me an average probability of $62.7\%$ with a standard deviation of $0.3\%$

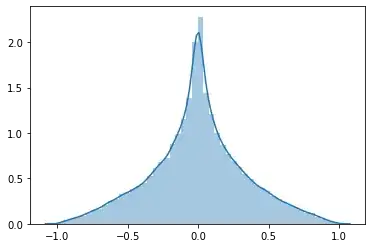
I plotted the simulated PDF and CDF. In that order, they are:

So I'm aiming to find a CDF that looks like the second image.

Theoretical Approach

The approach that I find easy to understand is outlined in this answer. Proceeding in a similar manner, we have

$$ f_A(a) = \begin{cases} \frac{1}{2}, &-1\leq a\leq+1\\ 0, &\text{ otherwise} \end{cases} $$

The PDFs are similar for $B$ and $C$.

The CDF for $A$ is

$$ F_A(a) = \begin{cases} \frac{a + 1}{2}, &-1\leq a\geq +1\\ 0,&a<-1\\ 1,&a>+1 \end{cases} $$

Let us assume $X=AC$. I proceed to calculate the CDF for $X$ (for $x>0$) as:

$$ \begin{align} F_X(x) &= P(X\leq x)\\ &= P(AC\leq x)\\ &= \int_{c=-1}^{+1}P(Ac\leq x)f_C(c)dc\\ &= \frac{1}{2}\left(\int_{c=-1}^{+1}P(Ac\leq x)dc\right)\\ &= \frac{1}{2}\left(\int_{c=-1}^{+1}P\left(A\leq \frac{x}{c}\right)dc\right)\\ \end{align} $$

We take a quick detour to make some observations. First, when $0<c<x$, we have $\frac{x}{c}>1$. Similarly, $-x<c<0$ implies $\frac{x}{c}<-1$. Also, $A$ is constrained to the interval $[-1, +1]$. Also, we're only interested when $x\geq 0$ because $B^2\geq 0$.

Continuing, the calculation

$$ \begin{align} F_X(x) &= \frac{1}{2}\left(\int_{c=-1}^{+1}P\left(A\leq \frac{x}{c}\right)dc\right)\\ &= \frac{1}{2}\left(\int_{c=-1}^{-x}P\left(A\leq \frac{x}{c}\right)dc + \int_{c=-x}^{0}P\left(A\leq \frac{x}{c}\right)dc + \int_{c=0}^{x}P\left(A\leq \frac{x}{c}\right)dc + \int_{c=x}^{+1}P\left(A\leq \frac{x}{c}\right)dc\right)\\ &= \frac{1}{2}\left(\int_{c=-1}^{-x}P\left(A\leq \frac{x}{c}\right)dc + 0 + 1 + \int_{c=x}^{+1}P\left(A\leq \frac{x}{c}\right)dc\right)\\ &= \frac{1}{2}\left(\int_{c=-1}^{-x}\frac{x+c}{2c}dc + 0 + 1 + \int_{c=x}^{+1}\frac{x+c}{2c}dc\right)\\ &= \frac{1}{2}\left(\frac{1}{2}(-x+x(\log(-x)-\log(-1)+1) + 0 + 1 + \frac{1}{2}(-x+x(-\log(x)-\log(1)+1)\right)\\ &= \frac{1}{2}\left(2 + \frac{1}{2}(-x+x(\log(x)) -x + x(-\log(x))\right)\\ &= 1 - x \end{align} $$

I don't think this is correct.

My Specific Questions

1. What mistake am I making? Can I even obtain the CDF through integration?
2. Is there an easier way? I used this approach because I was able to understand it well. There are shorter approaches possible (as is evident with the $\mathcal{U}(0,1)$ case) but perhaps I need to read more before I can comprehend them. Any pointers in the right direction would be helpful.

Answer 1

I would probably start by breaking into cases based on $A$ and $C$.

Conditioned on $A$ and $C$ having different signs, there are always real roots (because $4AC\leq 0$, so that $B^2-4AC\geq0$). The probability that $A$ and $C$ have different signs is $\frac{1}{2}$.

Conditioned on $A\geq0$ and $C\geq 0$, you return to the problem solved in the link above. Why? Because $B^2$ has the same distribution whether you have $B$ uniformly distributed on $(0,1)$ or on $(-1,1)$. At the link, they computed this probability as $\frac{5+3\log4}{36}\approx0.2544134$. The conditioning event here has probability $\frac{1}{4}$.

Finally, if we condition on $A<0$ and $C<0$, we actually end up with the same probability, as $4AC$ has the same distribution in this case as in the case where $A\geq0$ and $C\geq 0$. So, this is an additional $\frac{5+3\log 4}{36}\approx0.2544134$ conditional probability, and the conditioning event has probability $\frac{1}{4}$.

So, all told, the probability should be $$ \begin{align*} P(B^2-4AC\geq0)&=1\cdot\frac{1}{2}+\frac{1}{4}\cdot\frac{5+3\log4}{36}+\frac{1}{4}\cdot\frac{5+3\log 4}{36}\\ &=\frac{1}{2}+\frac{5+3\log4}{72}\\ &\approx0.6272... \end{align*} $$

Answer 2

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ Hereafter, $\ds{\bracks{P}}$ is an Iverson Bracket. Namely, $\ds{\bracks{P} = \color{red}{1}}$ whenever $\ds{P}$ is $\ds{\tt true}$ and $\ds{\color{red}{0}}$ $\ds{\tt otherwise}$. They are very convenient whenever we have to manipulate constraints.

---

\begin{align} &\bbox[5px,#ffd]{\int_{-1}^{1}{1 \over 2}\int_{-1}^{1} {1 \over 2}\int_{-1}^{1}{1 \over 2}\bracks{b^{2} - 4ac > 0} \dd c\,\dd a\,\dd b} \\[5mm] = &\ {1 \over 4}\int_{0}^{1}\int_{-1}^{1} \int_{-1}^{1}\bracks{b^{2} - 4ac > 0} \dd c\,\dd a\,\dd b \\[5mm] = &\ {1 \over 4}\int_{0}^{1}\int_{-1}^{1} \int_{0}^{1}\braces{\bracks{b^{2} - 4ac > 0} + \bracks{b^{2} + 4ac > 0}} \dd c\,\dd a\,\dd b \\[5mm] = &\ {1 \over 4}\int_{0}^{1}\int_{0}^{1} \int_{0}^{1}\left\{\bracks{b^{2} - 4ac > 0} + \bracks{b^{2} + 4ac > 0}\right. \\[2mm] &\ \phantom{{1 \over 4}\int_{0}^{1}\int_{-1}^{1} \int_{0}^{1}} \left. + \bracks{b^{2} + 4ac > 0} + \bracks{b^{2} - 4ac > 0}\right\}\dd c\,\dd a\,\dd b \\[5mm] = &\ {1 \over 2} + {1 \over 2}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1} \bracks{b^{2} - 4ac > 0}\dd c\,\dd a\,\dd b \\[5mm] = &\ {1 \over 2} + {1 \over 2}\int_{0}^{1}\int_{0}^{1}{1 \over a}\int_{0}^{a} \bracks{b^{2} - 4c > 0}\dd c\,\dd a\,\dd b \\[5mm] = &\ {1 \over 2} + {1 \over 2}\int_{0}^{1}\int_{0}^{1}\bracks{b^{2} - 4c > 0} \int_{c}^{1}{1 \over a}\,\dd a\,\dd c\,\dd b \\[5mm] = &\ {1 \over 2} - {1 \over 2}\int_{0}^{1}\int_{0}^{1} \bracks{c < {b^{2} \over 4}}\ln\pars{c}\,\dd c\,\dd b \\[5mm] = &\ {1 \over 2} - {1 \over 2}\int_{0}^{1}\int_{0}^{b^{2}/4} \ln\pars{c}\,\dd c\,\dd b \\[5mm] = &\ {1 \over 2} - {1 \over 2}\int_{0}^{1}\bracks{% -\,{1 + 2\ln\pars{2} \over 4}\,b^{2} + {1 \over 2}\,b^{2}\ln\pars{b}}\,\dd b \\[5mm] = & \bbx{{\ln\pars{2} \over 12} + {41 \over 72}} \approx 0.6272 \\ & \end{align}

Answer 3

We know from the quadratic formula that the polynomial $Ax^2 + Bx + C$ has real roots if $B^2 - 4AC \geq 0$. We can think of this problem in terms of volumes. To do so, it's easier if we rename the coefficients as $x \equiv A$, $y \equiv C$, and $z \equiv B$. Hence, in order to have real roots we require that $z^2 \geq 4xy$ for $x,y,z \in (-1,1)$. The probability we are after is the ratio between the volume of the region for which this inequality is true and the volume of the containing cube, which is 8. Begin by observing that if $x$ and $y$ have opposite signs then this inequality is trivially satisfied. The volume of the region for which they have opposite signs 4. Now consider the case where $x$ and $y$ have the same signs. In this case, we want to compute the volume above the surface $z^2 = 4xy$ and below the containing cube. There are four cases to consider:

1. $-1 < x \leq -\frac{1}{4}$ and $\frac{1}{4x} \leq y \leq 0$.
2. $-\frac{1}{4} \leq x \leq 0$ and $-1 < y \leq 0$.
3. $0 \leq x \leq \frac{1}{4}$ and $0 \leq y < 1$.
4. $\frac{1}{4} \leq x < 1$ and $0 \leq y \leq \frac{1}{4x}$.

By symmetry we can just consider cases 1 and 2 and then multiply that volume by 2. In each case we have to compute the integral: \begin{align*} \int_a^b\int_c^d 2 - 4\sqrt{xy}\,dy\,dx, \end{align*} where the limits of integration are defined above. Evaluating cases 1 and 2 we find that the volume is $5/18 + (1/6)\ln(4)$. Hence, the total volume that satisfies the inequality is \begin{align*} 4 + 2\left(\frac{5}{18} + \frac{1}{6}\ln(4)\right) = \frac{41}{9} + \frac{1}{3}\ln(4) \end{align*} which leads to a probability of \begin{align*} \frac{1}{8}\left(\frac{41}{9} + \frac{1}{3}\ln(4)\right) \approx 0.62721 \end{align*}