Evaluate the following integral $$ \tag1\int_{0}^{\frac{\pi}{2}}\frac1{(1+x^2)(1+\tan x)}\,\mathrm dx $$
My Attempt:
Letting $x=\frac{\pi}{2}-x$ and using the property that
$$ \int_{0}^{a}f(x)\,\mathrm dx = \int_{0}^{a}f(a-x)\,\mathrm dx $$
we obtain
$$ \tag2\int_{0}^{\frac{\pi}{2}}\frac{\tan x}{\left(1+\left(\frac{\pi}{2}-x\right)^2\right)(1+\tan x)}\,\mathrm dx $$
Now, add equation $(1)$ and $(2)$. After that I do not understand how I can proceed further.
Here is an approach.
We give some preliminary results.
The poly-Hurwitz zeta function may initially be defined by the series $$ \begin{align} \displaystyle \zeta(s\mid a,b) := \sum_{n=1}^{+\infty} \frac{1}{(n+a)^{s}(n+b)}, \quad \Re a >-1, \, \Re b >-1, \, \Re s>0. \tag1 \end{align} $$ This special function is a natural extension of the Hurwitz zeta function initially defined as $$ \zeta(s,a)=\sum_{n=0}^{\infty} \frac{1}{(n+a)^s}, \quad \Re a>0, \Re s>1, \tag2 $$ which is a natural extension itself of the Riemann zeta function initially defined as $$ \zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^s}, \quad \Re s>1. \tag3 $$
The poly-Hurwitz function appears in different places with different notations, one may find it here: [Masri, p. 2 and p. 15 (2004)], [Murty, p. 17 (2006)], [Sinha, p. 45 (2002)]. In this answer we are dealing with a simplified version of a general poly-Hurwitz function.
The series in $(1)$ converges absolutely for $\displaystyle \Re s>0$. Moreover, the convergence of the series is uniform on every half-plane $$\displaystyle H_{\delta}=\left\{s \in \mathbb{C}, \Re s \geq \delta \right\}, \, \delta \in \mathbb{R},\, \delta>0,$$ therefore the poly-Hurwitz zeta function $\displaystyle \zeta(\cdot \mid a,b)$ is analytic on the half-plane $\displaystyle \Re s>0$.
Let $a$, $b$ and $s$ be complex numbers such that $\Re a >-1, \, \Re b >-1, \, \Re s >0$. One may observe that $$ \begin{align} \zeta(s\mid a,b) & = \sum_{n=1}^{+\infty} \frac{1}{(n+a)^{s}(n+b)}\\ & = \sum_{n=1}^{+\infty} \frac{(n+b)+(a-b)}{(n+a)^{s+1}(n+b)}\\ & = \sum_{n=1}^{+\infty} \frac{1}{(n+a)^{s+1}}+(a-b)\sum_{n=1}^{+\infty} \frac{1}{(n+a)^{s+1}(n+b)} \tag4 \end{align} $$ giving the functional identity $$ \begin{align} \zeta(s \mid a,b) = \zeta(s+1,a+1) +(a-b) \zeta(s+1 \mid a,b) \tag5 \end{align} $$
where $\displaystyle \zeta(\cdot,\cdot)$ is the standard Hurwitz zeta function.
From $(5)$, we obtain by induction, for $n=1,2,3,\ldots $,
$$ \begin{align} \zeta(s\mid a,b) = \sum_{k=1}^{n}(a-b)^{k-1}\zeta(s+k,a+1) +(a-b)^n\zeta(s+n \mid a,b). \tag6 \end{align} $$
We use $(6)$ to extend $\displaystyle \zeta(\cdot \mid a,b)$ to a meromorphic function on each open set $\Re s>-n $, $n\geq 1$. Since the Hurwitz zeta function is analytic on the whole complex plane except for a simple pole at $1$ with residue $1$, then from $(6)$ the poly-Hurwitz zeta function $\displaystyle \zeta(\cdot\mid a,b)$ is analytic on the whole complex plane except for a simple pole at $0$ with residue $1$.
In 1885 Stieltjes has found that the Laurent series expansion around $1$ of the Riemann zeta function $$ \zeta(1+s) = \frac{1}{s} + \sum_{k=0}^{\infty} \frac{(-1)^{k}}{k!}\gamma_k s^k, \quad s \neq 0,\tag7 $$ is such that the coefficients of the regular part of the expansion are given by $$ \begin{align} \gamma_k& = \lim_{N\to \infty}\left(\sum_{n=1}^N \frac{\log^k n}{n}-\frac{\log^{k+1} \!N}{k+1}\right). \end{align} \tag8 $$ Euler was the first to define a constant of this form (1734) $$ \begin{align} \gamma & = \lim_{N\to\infty}\left(1+\frac12+\frac13+\cdots+\frac1N-\log N\right)=0.577215\ldots. \end{align} $$ The constants $\displaystyle \gamma_k$ are called the Stieltjes constants and due to the fact that $\displaystyle \gamma_0=\gamma$ they are sometimes called the generalized Euler's constants.
Similarly, Wilton (1927) and Berndt (1972) established that the Laurent series expansion in the neighbourhood of $1$ of the Hurwitz zeta function $$ \begin{align} \zeta(1+s,a) = \frac1s+\sum_{k=0}^{\infty}\frac{(-1)^{k}}{k!} \gamma_{k}(a)\:s^{k}, \quad \Re a>0, \,s\neq 0, \tag{9} \end{align} $$ is such that the coefficients of the regular part of the expansion are given by $$ \begin{align} \gamma_k(a)& = \lim_{N\to \infty}\left(\sum_{n=0}^N \frac{\log^k (n+a)}{n+a}-\frac{\log^{k+1} (N+a)}{k+1}\right), \quad \Re a>0, \end{align} \tag{10} $$ with $\displaystyle \gamma_{0}(a)=-\psi(a)=-\Gamma'(a)/\Gamma(a)$. The coefficients $\gamma_k(a)$ are called the generalized Stieltjes constants.
We have seen from $(6)$ that the poly-Hurwitz zeta function admits a Laurent series expansion around $0$. Let's denote by $\displaystyle\gamma_k(a,b)$ the coefficients of the regular part of $\displaystyle \zeta(\cdot\mid a,b)$ around $0$. I will call these coefficients the poly-Stieltjes constants.
Do we have an analog of $(10)$ for $\displaystyle\gamma_k(a,b)$?
The following result is new.
Theorem 1. Let $a,b$ be complex numbers such that $\Re a >-1, \, \Re b >-1$. Consider The poly-Hurwitz zeta function $$ \begin{align} \zeta(s\mid a,b) := \sum_{n=1}^{+\infty} \frac{1}{(n+a)^{s}(n+b)}, \quad \Re s>0. \tag{11} \end{align} $$ Then the meromorphic extension of $\displaystyle \zeta(\cdot\mid a,b)$ admits the following Laurent series expansion around $0$, $$ \zeta(s \mid a,b) = \frac{1}{s} + \sum_{k=0}^{+\infty} \frac{(-1)^{k}}{k!}\gamma_k(a,b) s^k, \quad s \neq 0,\tag{12} $$ where the poly-Stieltjes constants $\displaystyle \gamma_k(a,b)$ are given by $$ \begin{align} \gamma_k(a,b)& = \lim_{N\to+\infty}\left(\sum_{n=1}^N \frac{\log^k (n+a)}{n+b}-\frac{\log^{k+1} \!N}{k+1}\right) \end{align} \tag{13} $$ with $$ \gamma_{0}(a,b)=-\psi(b+1)=-\Gamma'(b+1)/\Gamma(b+1). \tag{14}$$
Proof. Let $a,b$ be complex numbers such that $\Re a >-1, \, \Re b >-1$.
We first assume $\Re s>0$. Observing that, for each $n \geq 1$, $$ \left|\sum_{k=0}^{\infty}\frac{\log^k(n+a)}{n+b}\frac{(-1)^{k}}{k!}s^k\right| \leq \sum_{k=0}^{\infty}\left|\frac{\log^k(n+a)}{n+b}\right|\frac{|s|^k }{k!}<\infty $$ and that $$ \sum_{n=1}^{\infty}\left|\sum_{k=0}^{\infty}\frac{\log^k(n+a)}{n+b}\frac{(-1)^{k}}{k!}s^k\right|=\sum_{n=1}^{\infty}\left|\frac1{(n+a)^s(n+b)}\right| = \sum_{n=1}^{\infty}\frac1{|n+a|^{\Re s}|n+b|}<\infty,$$ we obtain $$ \begin{align} &\sum_{k=0}^{\infty}\frac{(-1)^{k}}{k!}\lim_{N\to+\infty}\left(\sum_{n=1}^N\frac{\log^k(n+a)}{n+b}-\frac{\log^{k+1} \!N}{k+1}\right) s^k \\\\ &= \lim_{N\to+\infty}\sum_{k=0}^{\infty} \frac{(-1)^{k}}{k!}\left(\sum_{n=1}^N\frac{\log^k(n+a)}{n+b}-\frac{\log^{k+1} \!N}{k+1}\right) s^k \\\\ &=\lim_{N\to+\infty}\sum_{k=0}^{\infty}\left(\sum_{n=1}^N\frac{(-1)^{k}}{k!}\frac{\log^k(n+a)}{n+b}s^k -\frac{(-1)^{k}}{k!}\frac{\log^{k+1} \!N}{k+1}s^k\right) \\\\ &=\lim_{N\to+\infty}\left(\sum_{n=1}^N\sum_{k=0}^{\infty}\frac{(-1)^{k}}{k!}\frac{\log^k(n+a)}{n+b}s^k -\sum_{k=0}^{\infty}\frac{(-1)^{k}}{k!}\frac{\log^{k+1} \!N}{k+1}s^k\right) \\\\ &=\lim_{N\to+\infty}\left(\sum_{n=1}^N\frac1{(n+a)^s(n+b)} +\frac1{N^s}-\frac1s\right) \\\\ &=\zeta(s \mid a,b)-\frac1{s} \end{align} $$ as desired. Then, using $(6)$, we extend the preceding identity by analytic continuation to all $s \neq 0$. To prove $(14)$, we start from a standard series representation of the digamma function (see Abram. & Steg. p. 258 6.3.16): $$ \begin{align} -\psi(b+1) &= \gamma - \sum_{n=1}^{\infty} \left( \frac1n - \frac1{b+n} \right) \\ &=\lim_{N\to+\infty}\left(\gamma - \sum_{n=1}^N\left( \frac1n - \frac1{b+n} \right)\right)\\ &=\lim_{N\to+\infty}\left(\left(\sum_{n=1}^N\frac1{b+n} -\ln N\right)-\left(\sum_{n=1}^N\frac1n-\ln N-\gamma \right)\right)\\ &=\lim_{N\to+\infty}\left(\sum_{n=1}^N\frac1{b+n} -\ln N\right)\\\\ &=\gamma_0(a,b) \end{align} $$ using $(13)$.
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Box$
One of the consequences of Theorem 1 is the new possibility to express some series in terms of the poly-Stieltjes constants.
Theorem 2. Let $a,b,c$ be complex numbers such that $\Re a >-1, \, \Re b >-1, \, \Re c >-1$.
Then $$ \begin{align} (b-a)\sum_{n=1}^{+\infty} \frac{\log (n+c)}{(n+a)(n+b)}=\gamma_1(c,a)-\gamma_1(c,b), \tag{15} \end{align} $$ similarly $$ \begin{align} \sum_{n=1}^{+\infty} \frac1{n+b}\left({\log (n+a)-\log (n+c)}\right)=\gamma_1(a,b)-\gamma_1(c,b), \tag{16} \end{align} $$ with the poly-Stieltjes constant $$\gamma_1(a,b) = \lim_{N\to+\infty}\left(\sum_{n=1}^N \frac{\log (n+a)}{n+b}-\frac{\log^2 \!N}2\right). $$
Proof. Let $a,b,c$ be complex numbers such that $\Re a >-1, \, \Re b >-1, \, \Re c >-1$.
We have $$ (b-a)\frac{\log (n+c)}{(n+a)(n+b)}=\frac{\log (n+c)}{n+a}-\frac{\log (n+c)}{n+b} $$ giving, for $N\geq1$, $$ \begin{align} (b-a)&\sum_{n=1}^N \frac{\log (n+c)}{(n+a)(n+b)}=\\\\ & \left(\sum_{n=1}^N\frac{\log (n+c)}{n+a}-\frac{\log^2 \!N}2\right)-\left(\sum_{n=1}^N\frac{\log (n+c)}{n+b}-\frac{\log^2 \!N}2\right) \tag{17} \end{align} $$ letting $N \to \infty$ and using $(13)$ gives $(15)$.
We have, for $N\geq1$, $$ \begin{align} &\sum_{n=1}^N \frac1{n+b}\left({\log (n+a)-\log (n+c)}\right)\\\\ &= \left(\sum_{n=1}^N\frac{\log (n+a)}{n+b}-\frac{\log^2 \!N}2\right)-\left(\sum_{n=1}^N\frac{\log (n+c)}{n+b}-\frac{\log^2 \!N}2\right) \tag{18} \end{align} $$ letting $N \to \infty$ and using $(13)$ gives $(16)$.
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Box$
Let’s first give a numerical evaluation of Juantheron’s integral.
I would like to thank Jonathan Borwein and David H. Bailey who obtained the result below to $1000$ digits, in just 3.9 seconds run time, using David's new MPFUN-MPFR software, along with the tanh-sinh quadrature program included with the MPFUN-MPFR package.
They also tried the integral with David's MPFUN-Fort package, which has a completely different underlying multiprecision system, and they obtained the same result below.
Finally, they computed the integral with Mathematica $11.0$; it agreed with the result below, although it required about 10 times longer to run.
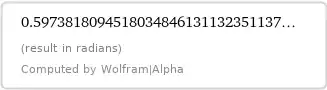
Proposition 1. We have $$ \begin{align} \int_{0}^{\Large\frac{\pi}2}\!&\frac1{(1+x^2)(1+\tan x)}\mathrm dx\\\\= 0.&59738180945180348461311323509087376430643859042555\\ &67307703207161550311033249824121789098990404474443\\ &73300942847961727020952797366230453350097928752529\\ &62099371263365268445580755896768905606293308536674\\ &89639352215352393870280616186538538722285601087082\\ &81730013060929540132583577240799018025603130403772\\ &83596189879605956759516344861849456740112012597646\\ &30195536341071109827787231788650530475635336662512\\ &50757672078320586388500276160658476344052492489409\\ &64026178233152015087197531148322444147655936720008 \tag{19}\\ &40650450631581050321100329502169853063154902765446\\ &58804861176982696627707544105655815406116180984371\\ &54148587721902800400109013880620460529382772599713\\ &06874977209651994186527207589425408866256042399213\\ &80515694164361264997143539392018681691584285790381\\ &65536517701019826846772718498479534803417547866296\\ &23842162877309354675086691711521468623807334908897\\ &71491673168051054009130049879837629516862688171756\\ &13790927986073268994254629238035029442300668334396\\ &901581838911515359223628586133156893962372426055\cdots \end{align} $$
David H. Bailey confirmed that Mathematica $11.0$, in spite of the great numerical precision, could not find a closed-form of the integral.
The next result proves that the OP integral admits a closed form in terms of the poly-Stieltjes constants.
Proposition 2. We have $$ \begin{align} \int_{0}^{\Large\frac{\pi}2}\!\!\frac1{(1+x^2)(1+\tan x)}\mathrm dx &=\frac{(e^2+1)^2}{2(e^4+1)}\arctan \! \frac{\pi}{2}-\frac{e^4-1}{4(e^4+1)}\log\left(1+\frac{\pi^2}{4}\right)\\\\ &+\frac{64 \pi^2\log 3}{(\pi^2+16)(9\pi^2+16)} \\\\ &+\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac34,\frac34 +\frac{i}{\pi}\!\right) -\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac14,\frac34 +\frac{i}{\pi}\!\right)\tag{20}\\\\ &+\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac34,\frac14 -\frac{i}{\pi}\!\right) -\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac14,\frac14 -\frac{i}{\pi}\!\right) \end{align} $$ with the poly-Stieltjes constant $$\gamma_1(a,b) = \lim_{N\to+\infty}\left(\sum_{n=1}^N \frac{\log (n+a)}{n+b}-\frac{\log^2 \!N}2\right). $$
Proof. We proceed in three steps.
Step 1. One may write $$ \require{cancel} \begin{align} &\int_{0}^{\Large\frac{\pi}{2}}\frac{1}{(1+x^2)(1+\tan x)}\mathrm dx \\ &=\int_{0}^{\Large\frac{\pi}{2}}\frac{\cos x}{(1+x^2)(\cos x+\sin x)}\mathrm dx\\ &=\frac12\int_{0}^{\Large\frac{\pi}{2}}\frac{(\cos x+\sin x)+(\cos x-\sin x)}{(1+x^2)(\cos x+\sin x)}\mathrm dx\\ &=\frac12\int_{0}^{\Large\frac{\pi}{2}}\!\frac{1}{1+x^2}\mathrm dx+\frac12\int_{0}^{\Large\frac{\pi}{2}}\frac{1}{(1+x^2)}\frac{(\cos x-\sin x)}{(\cos x+\sin x)}\mathrm dx\\ &=\frac12 \arctan\! \frac{\pi}{2}+\frac12\int_{0}^{\Large\frac{\pi}{2}}\frac{1}{1+x^2}\tan (x-\pi/4)\:\mathrm dx\\ &=\frac12 \arctan\! \frac{\pi}{2}+\frac12\int_{-\Large\frac{\pi}{4}}^{\Large\frac{\pi}4}\frac{1}{1+(x+\pi/4)^2}\tan x \:\mathrm dx\\ &=\frac12 \arctan\! \frac{\pi}{2}+\frac12\int_0^{\Large\frac{\pi}4}\left(\frac1{1+(x+\pi/4)^2}-\frac1{1+(x-\pi/4)^2}\right)\tan x \:\mathrm dx\\ &=\frac12 \arctan\! \frac{\pi}{2}-\frac{\Im}2 \!\int_{0}^{\Large\frac{\pi}{4}}\!\!\left(\!\frac1{x+\pi/4+i}+\frac1{x-\pi/4-i}\!\right) \tan x \:\mathrm dx \tag{21} \end{align} $$ Let’s evaluate the latter integral.
Step 2. One may recall that the tangent function, as a meromorphic function, can be expressed as an infinite sum of rational functions: $$ \tan x = \sum_{n=0}^{+\infty} \frac{2x}{\pi^2 (n+1/2)^2-x^2}, \quad x \neq \pm \pi/2, \pm 3\pi/2,\pm 5\pi/2,\ldots. \tag{22} $$ We have the inequality $$ \sup_{x \in [0,\pi/4]}\left|\frac{2x}{\pi^2 (n+1/2)^2-x^2}\right|\leq \frac1{(n+1/2)^2}, \quad n=0,1,2,\ldots, \tag{23} $$ the convergence in $(22)$ is then uniform on $[0,\pi/4]$. Thus, plugging $(22)$ into $(21)$, we are allowed to integrate $(21)$ termwise.
Each term, via a partial fraction decomposition, is evaluated to obtain $$ \begin{align} \int_{0}^{\Large\frac{\pi}4}\!&\left(\!\frac1{x+\pi/4+i}+\frac1{x-\pi/4-i}\!\right)\frac{2x}{\pi^2 (n+1/2)^2-x^2}\:\mathrm dx\\ &=\frac{2\tau}{\pi^2 (n+1/2)^2-\tau^2}\log \left( \frac{4\tau-\pi}{4\tau+\pi}\right)\\ &+\frac1{\pi}\frac1{(n+1/2+\tau/\pi)}\left(\log\!\left(n+\frac34\right)-\log\!\left(n+\frac14\right) \right)\\ &+\frac1{\pi}\frac1{(n+1/2-\tau/\pi)}\left(\log\!\left(n+\frac34\right)-\log\!\left(n+\frac14\right) \right) \end{align} \tag{24} $$ where for the sake of convenience we have set $\tau:=\pi/4+i$.
Step 3. We sum $(24)$ from $n=0$ to $\infty$ obtaining
$$ \begin{align} \int_{0}^{\Large\frac{\pi}{4}}\!&\left(\!\frac1{x+\pi/4+i}+\frac1{x-\pi/4-i}\!\right) \tan x \:\mathrm dx\\ &=\sum_{n=0}^{\infty}\frac{2\tau}{\pi^2 (n+1/2)^2-\tau^2}\log \left( \frac{4\tau-\pi}{4\tau+\pi}\right)\\ &+\frac1{\pi}\sum_{n=0}^{\infty}\frac1{(n+1/2+\tau/\pi)}\left(\log\!\left(n+\frac34\right)-\log\!\left(n+\frac14\right) \right)\\ &+\frac1{\pi}\sum_{n=0}^{\infty}\frac1{(n+1/2-\tau/\pi)}\left(\log\!\left(n+\frac34\right)-\log\!\left(n+\frac14\right) \right), \tag{25} \end{align} $$ then, singling out the first terms in the two last series and using Theorem $2$ $(16)$, we get $$ \begin{align} \int_{0}^{\Large\frac{\pi}{4}}\!&\left(\!\frac1{x+\pi/4+i}+\frac1{x-\pi/4-i}\!\right) \tan x \:\mathrm dx\\ &=\tan \tau \log \left( \frac{4\tau-\pi}{4\tau+\pi}\right) +\frac{4\pi}{\pi^2 -4\tau^2}\log 3 \\&+\frac1{\pi}\gamma_1\!\left(\!\frac34,\frac12 +\frac{\tau}{\pi}\!\right) -\frac1{\pi}\gamma_1\!\left(\!\frac14,\frac12 +\frac{\tau}{\pi}\!\right)\tag{26}\\ &+\frac1{\pi}\gamma_1\!\left(\!\frac34,\frac12 -\frac{\tau}{\pi}\!\right) -\frac1{\pi}\gamma_1\!\left(\!\frac14,\frac12 -\frac{\tau}{\pi}\!\right) \end{align} $$ and the substitution $\tau=\pi/4+i$ gives the desired result.
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Box$
Achille Hui's conjecture is true.
Achille Hui has announced in the comments that the OP integral is equal to $$ \begin{align} \frac{\arctan(\frac{\pi}{2}) - t\log\sqrt{1+\frac{\pi^2}{4}}}{1+t^2}+\frac{\pi^2}4 \sum_{n=0}^{\infty}\frac{ (2n+1)\left(\log\left(n+\frac34\right)-\log\left(n+\frac14\right)\right) }{ \left(1+\pi^2\left(n+\frac14\right)^2\right)\left(1+\pi^2\left(n+\frac34\right)^2\right) } \tag{27} \end{align} $$ with $\displaystyle t := \tanh(1)$.
The first term in $(27)$, with a little algebra is seen to be equal to the sum of the first two terms on the right hand side of $(20)$.
We establish the veracity of the conjecture using Proposition $2$ and using the next result.
Proposition 3. We have $$ \begin{align} &\frac{\pi^2}4 \sum_{n=0}^{\infty}\frac{ (2n+1)\left(\log\left(n+\frac34\right)-\log\left(n+\frac14\right)\right) }{ \left(1+\pi^2\left(n+\frac14\right)^2\right)\left(1+\pi^2\left(n+\frac34\right)^2\right) }\\\\ &=\frac{64 \pi^2\log 3}{(\pi^2+16)(9\pi^2+16)} \\\\ &+\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac34,\frac34 +\frac{i}{\pi}\!\right) -\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac14,\frac34 +\frac{i}{\pi}\!\right)\tag{28}\\\\ &+\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac34,\frac14 -\frac{i}{\pi}\!\right) -\frac{\Im}{2\pi}\gamma_1\!\left(\!\frac14,\frac14 -\frac{i}{\pi}\!\right) \end{align} $$ with the poly-Stieltjes constant $$\gamma_1(a,b) = \lim_{N\to+\infty}\left(\sum_{n=1}^N \frac{\log (n+a)}{n+b}-\frac{\log^2 \!N}2\right).$$
Proof. Observe that the first term of the series on the left hand side of $(28)$, given by $n=0$, is just equal to $$ \frac{64 \pi^2\log 3}{(\pi^2+16)(9\pi^2+16)}. $$ By a partial fraction decomposition, one may check that $$ \begin{align} \frac{\pi^2}4 &\frac{ (2n+1) }{ \left(1+\pi^2\left(n+\frac14\right)^2\right)\left(1+\pi^2\left(n+\frac34\right)^2\right) } =\frac{\Im}{2\pi}\left(\!\frac1{n+\frac34+\frac{i}{\pi}}-\frac1{n+\frac14+\frac{i}{\pi}}\!\right) \tag{29} \end{align} $$ then, multiplying $(29)$ by $\left(\log\!\left(n+\frac34\right)-\log\!\left(n+\frac14\right)\right)$ and summing from $n=1$ to $\infty$ we get, using Theorem $2$ $(16)$, the result $(28)$.
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \Box$
Too long for a comment: It is known that $\displaystyle\int_0^\frac\pi2\sin(\sin x)dx=\int_0^\frac\pi2\sin(\cos x)dx=\frac\pi2H_0(1)$,
and $\displaystyle\int_0^\frac\pi2\cos(\cos x)dx=\int_0^\frac\pi2\cos(\sin x)dx=\frac\pi2J_0(1)$, where H and J are the Struve and Bessel
functions respectively, so it is not out of the question that the existence of such closed forms, at
least in terms of these special functions, might have been one of the main initial triggers which
determined our anonymous source to investigate the nature of $\displaystyle\int_0^\frac\pi2\!\tan(\tan x)dx$, which turns
out to be $\ldots$ rather difficult, to say the very least. Indeed, the entire interval $\bigg(0,\dfrac\pi2\bigg)$ can be
broken up into an infinite number of sub-intervals, the first one of which is $\bigg(0,~\arctan\dfrac\pi2\bigg)$,
while all others are of the form $\bigg[\arctan\bigg(\dfrac\pi2+k\pi\bigg),~\arctan\bigg(\dfrac\pi2+\big(k+1\big)\pi\bigg)\bigg]$, for $k\in$ N.
The integral diverges towards $+\infty$ on the former, and towards $-\infty$ on the rest, but in such
a manner that $\displaystyle\int_0^{\alpha(k)}\!\tan(\tan x)dx\to\infty$ rather than $-\infty$, where $\alpha(k)=\arctan\bigg(\dfrac\pi2+k\pi\bigg)$.
This can be better visualized by plotting the function's graphic. But determining whether the
limit $\displaystyle\lim_{k\to\infty}\int_0^{\alpha(k)}\!\tan(\tan x)dx$ ultimately converges or diverges is by no means a trivial task
$\big($indeed, it is quite daunting$\big)$, so, discouraged, either by the integral's probable divergence, or
perhaps by its difficulty, or maybe by a bit of both, our anonymous source $\big($let's call him/her
Person X$\big)$ decides to focus its attention now on $\bigg(0,~\arctan\dfrac\pi2\bigg)$, but not before changing the
function into $~\dfrac1{\tan(\tan x)}$ , so as to avoid its divergence in $x=\arctan\dfrac\pi2$ . However, he now
faces another problem: its divergence in $0$. In order to fix this new impediment, the function
is further changed to $~\dfrac1{1+\tan(\tan x)}$ . Then, by a simple substitution, $\displaystyle\int_0^{\alpha(0)}\frac{dx}{1+\tan(\tan x)}$
becomes $\displaystyle\int_0^\frac\pi2\frac{dx}{(1+x^2)(1+\tan x)}$ , as already pointed out by ncmathsadist in the comment
section above. That such an improvised integral would indeed have a meaningful closed form
is no more likelier than for $\displaystyle\int_0^\frac\pi2\frac{dx}{1+\sin(\sin x)}=\int_0^\frac\pi2\frac{dx}{1+\sin(\cos x)}$ or $\displaystyle\int_0^\frac\pi2\frac{dx}{1+\cos(\cos x)}$
$=\displaystyle\int_0^\frac\pi2\frac{dx}{1+\cos(\sin x)}$ to possess one as well.
It is clear that the integral cannot be expressed in the form of elementary functions. This is another approach expanding on mwomath's comment. I feel this approach may be useful as it is a bit easier to understand in my opinion, as compared to Olivier Oloa's answer (which is completely fine). Sorry in advance for any steps I miss.
$$\int_0^{\pi/2} \frac{dx}{(1+x^2)(1+\tan x)}$$ $$=\int_0^{\pi/2} \frac{\cos x dx}{(1+x^2)(\sin x+\cos x)}$$ $$= \int_0^{\pi/2} \frac{\cos x dx}{(1+x^2)(\sin x+\cos x)}.\frac{(\cos x-\sin x)}{(\cos x-\sin x)}$$ $$=\int_0^{\pi/2} \frac{\cos^2 x-\sin x \cos x }{(1+x^2)(\cos^2 x-\sin^2 x)}dx$$ $$=\int_0^{\pi/2} \frac{\cos^2 x-\sin x \cos x }{(1+x^2)(\cos 2x)}dx$$ $$=\int_0^{\pi/2} \frac{1}{2}\frac{(2\cos^2 x-1-2\sin x \cos x+1) }{(1+x^2)(\cos 2x)}dx$$ $$=\int_0^{\pi/2} \frac{1}{2}\frac{(\cos 2x-\sin 2x+1) }{(1+x^2)(\cos 2x)}dx$$
$$=\int_0^{\pi/2}\frac{1}{1+x^2}dx+\int_0^{\pi/2}\frac{\sec 2x}{1+x^2}dx-\int_0^{\pi/2}\frac{\tan 2x}{1+x^2}dx$$
We know that $\int \frac{1}{1+x^2}dx=\arctan x$
So, $$\int_0^{\pi/2}\frac{1}{1+x^2}dx=\arctan (\pi/2)$$
The infinite sum of $\sec x$ is given as:
$$\sec x =\sum_{n=0}^{\infty} \frac{U_{2n}x^{2n}}{(2n)!}$$ where $U_{n}$ up/down number.
Similarly, $$\int_0^{\pi/2}\frac{\sec 2x}{1+x^2}dx=\int_0^{\pi/2} \sum_{n=0}^{\infty} \frac{2^n.U_{2n}x^{2n}}{(2n)!(1+x^2)}dx= \sum_{n=0}^{\infty} \int_0^{\pi/2} \frac{2^{2n}.U_{2n}x^{2n}}{(2n)!(1+x^2)}dx$$ $$\int \frac{x^{2n}}{1+x^2}dx=\frac{x^{2n+1}}{2n+1}\left( 1+\frac{2n+1}{2n+3}(-x^2)+\frac{2n+1}{2n+5}(-x^2)^2-\frac{2n+1}{2n+7}(-x^2)^6+\cdots\right)$$
We can express the infinite sum in the parenthesis in form of the hyper-geometric function:
$$_2F_1 \left(1, n+\frac{1}{2}; n+\frac{3}{2} ; -x^2 \right)$$
So, $$\int_0^{\pi/2}\frac{\sec 2x}{1+x^2}dx=\sum_{n=0}^{\infty} \int_0^{\pi/2} \frac{2^{2n}.U_{2n}x^{2n}}{(2n)!(1+x^2)}dx$$ $$= \sum_{n=0}^{\infty} \frac{2^{2n}.U_{2n}}{(2n)!}\frac{(\pi/2)^{2n+1}}{(2n+1)}._2F_1 \left(1, n+\frac{1}{2}; n+\frac{3}{2} ; -\pi^2/4 \right)$$
The infinite sum of $\tan x$ is given as: $$\tan x =\sum_{n=0}^{\infty} \frac{U_{2n+1}x^{2n+1}}{(2n+1)!}$$ where $U_{n}$ up/down number.
Similarly, $$\int_0^{\pi/2}\frac{\tan 2x}{1+x^2}dx=\int_0^{\pi/2} \sum_{n=0}^{\infty} \frac{2^{2n+1}.U_{2n+1}x^{2n+1}}{(2n+1)!(1+x^2)}dx= \sum_{n=0}^{\infty} \int_0^{\pi/2} \frac{2^{2n+1}.U_{2n+1}x^{2n+1}}{(2n+1)!(1+x^2)}dx$$ $$\int \frac{x^{2n+1}}{1+x^2}dx=\frac{x^{2n+2}}{2n+2}\left( 1+\frac{2n+2}{2n+4}(-x^2)+\frac{2n+2}{2n+6}(-x^2)^2-\frac{2n+2}{2n+8}(-x^2)^6+\cdots\right)$$
We can express the infinite sum in the parenthesis in form of the hyper-geometric function:
$$_2F_1 \left(1, n+1; n+2 ; -x^2 \right)$$
So, $$\int_0^{\pi/2}\frac{\tan 2x}{1+x^2}dx=\sum_{n=0}^{\infty} \int_0^{\pi/2} \frac{2^{2n+1}.U_{2n+1}x^{2n+1}}{(2n+1)!(1+x^2)}dx$$ $$= \sum_{n=0}^{\infty} \frac{2^{2n+1}.U_{2n+1}}{(2n+1)!}\frac{(\pi/2)^{2n+2}}{(2n+2)}._2F_1 \left(1, n+1; n+2 ; -\pi^2/4 \right)$$
$$\int_0^{\pi/2} \frac{dx}{(1+x^2)(1+\tan x)}$$ $$=\sum_{n=0}^{\infty} \frac{2^{2n}.U_{2n}}{(2n)!}\frac{(\pi/2)^{2n+1}}{(2n+1)}._2F_1 \left(1, n+\frac{1}{2}; n+\frac{3}{2} ; -\pi^2/4 \right)$$ $$+\sum_{n=0}^{\infty} \frac{2^{2n+1}.U_{2n+1}}{(2n+1)!}\frac{(\pi/2)^{2n+2}}{(2n+2)}._2F_1 \left(1, n+1; n+2 ; -\pi^2/4 \right)+\arctan (\pi/2) + C$$
or if you don't want to use hyper-geometric functions (in my opinion they just make the integral look a bit more clean and are a good way of representing certain infinite sums):
$$\int_0^{\pi/2} \frac{dx}{(1+x^2)(1+\tan x)}$$ $$=\sum_{n=0}^{\infty} \left( \frac{2^{2n}.U_{2n}.(\pi/2)^{2n}}{(2n)!}.\sum_{k=0}^{\infty}\frac{(-1)^{k}(\pi/2)^{2k+1}}{2(n+k)+1} \right)$$ $$+\sum_{n=0}^{\infty} \left(\frac{2^{2n+1}.U_{2n+1}(\pi/2)^n}{(2n+1)!} .\sum_{k=1}^{\infty}\frac{(-1)^{k-1}(\pi/2)^{2k}}{2(n+k)}\right) +\arctan (\pi/2) + C$$
Let us try to understand the computer-based answer of Oliver Oloa.
Rational decomposition.
Is known the rational decomposition of the trigonometric functions in the forms of $$\tan z = \sum\limits_{n=0}^\infty\dfrac{8z}{\pi^2\left(2n+1\right)^2 - 4z^2},\tag{R1}$$ $$\sec z = \sum\limits_{n=0}^\infty (-1)^n\dfrac{4\pi(2n+1)}{\pi^2\left(2n+1\right)^2 - 4z^2},\tag{R2}$$ with the corollaries $$\tanh z =-i\tan(iz) = \sum\limits_{n=0}^\infty\dfrac{8z}{\pi^2\left(2n+1\right)^2 + 4z^2},\tag{R3}$$ $$\operatorname{sech}z = \sec(iz) = \sum\limits_{n=0}^\infty (-1)^n\dfrac{4\pi(2n+1)}{\pi^2\left(2n+1\right)^2 + 4z^2}.\tag{R4}$$
Preparation.
$$I=\int\limits_0^{\Large^\pi/_2}\dfrac{\text dx}{(1+x^2)(1+\tan x)} =\dfrac12\int\limits_0^{\Large^\pi/_2}\left(\dfrac{1+\tan x}{1+\tan x} -\dfrac{\tan x-1}{1+\tan x}\right)\,\dfrac{\text dx}{1+x^2}$$ $$=\dfrac12\int\limits_0^{\Large^\pi/_2}\dfrac{\text dx}{1+x^2} -\dfrac12\int\limits_0^{\Large^\pi/_2}\tan\left(x-\dfrac\pi4\right)\,\dfrac{\text dx}{1+x^2},$$ $$I=\dfrac12\int\limits_0^{\Large^\pi/_2}\dfrac{\text dx}{1+x^2} -\dfrac12\int\limits_0^{\Large^\pi/_2}\sum\limits_{n=0}^\infty g_n(x)\,\text dx,\tag1$$ where, taking in account $(R1),$ $$g_n(x)=\dfrac{2x-\large\frac\pi2}{\pi^2\left(n+\large\frac12\right)^2 - \left(x-\large\frac\pi4\right)^2}\cdot\dfrac1{1+x^2}.\tag2$$
Partial fractions.
The functions $\;g_n(x)\;$ allow decomposition in the form of $$g_n(x)=\dfrac{A_nx+B_n}{1+x^2} + \dfrac {C_n}{\pi n+\frac34\pi-x} + \dfrac {D_n}{\pi n+\frac14\pi+x}.\tag3$$ Then $$C_n=\lim_{\large x\to \pi n+\frac34\pi}\, \left(\pi n+\frac34\pi-x\right)g_n(x) = \dfrac{16}{(4 n\pi+3\pi)^2 +16},$$ $$D_n=\lim_{\large x\to -\pi n-\frac14\pi}\, \left(\pi n+\frac14\pi+x\right)g_n(x) = -\dfrac{16}{(4n\pi+\pi)^2 +16},$$ $$A_n-C_n+D_n=\lim_{\large x\to \infty}\, x g_n(x) = 0,\quad A_n=C_n-D_n,$$ $$B_n+ \dfrac {C_n}{\pi n+\frac34\pi} + \dfrac {D_n}{\pi n+\frac14\pi} =g_n(0) = -\dfrac8{\pi(16n^2+16n+3)},$$ $$B_n = \dfrac4{4\pi n+3\pi} -\dfrac4{4\pi n+\pi} - \dfrac {4C_n}{4\pi n+3\pi} - \dfrac {4D_n}{4\pi n+\pi}.$$ $$B_n = 4(4\pi n+3\pi)C_n + 4(4\pi n+\pi)D_n.$$
Let $$U_k = \dfrac{16}{(2k\pi+\pi)^2+16},$$ then, taking in account $(R3)-(R4),$ $$D_n = -U_{2n},\quad C_n=U_{2n+1},\;$$ $$\sum\limits_{n=0}^\infty A_n = \sum\limits_{n=0}^\infty U_n = \tanh2,\tag4$$ $$\sum\limits_{n=0}^\infty B_n = \sum\limits_{n=0}^\infty (-1)^{n+1}4\pi(2n+1)U_n = -\operatorname{sech}2.\tag5$$
Integration.
$$I=\dfrac12\int\limits_0^{\Large^\pi/_2}\dfrac{\text dx}{1+x^2} -\dfrac12\int\limits_0^{\Large^\pi/_2}\sum\limits_{n=0}^\infty g_n(x)\,\text dx$$ $$ = \dfrac12 \arctan \,\dfrac\pi2-\dfrac12\sum\limits_{n=0}^\infty \left(\dfrac12 A_n \ln\left(\dfrac{\pi^2}4+1\right) +B_n \arctan \,\dfrac\pi2+(C_n+D_n) \ln\dfrac{4n + 3}{4n+1}\right),$$ $$I=-\dfrac14\tanh 2\ln\left(\dfrac{\pi^2}4+1\right) + \dfrac{1+\operatorname{sech}2}2 \arctan \,\dfrac\pi2-\dfrac12 I_1,\tag6$$ where $$I_1=\sum\limits_{n=0}^\infty (C_n+D_n) \ln\dfrac{4n + 3}{4n+1},\tag7$$ with the representations $$I_1=\sum\limits_{n=0}^\infty \dfrac{128\pi^2(2n+1)}{\pi^4((4n+2)^2-1)^2 +32\pi^2((4n+2)^2+1)+256}\,\ln\dfrac{4n+3}{4n+1}\tag{7a}$$
and $$I_1=\sum\limits_{n=0}^\infty \Im\left(-\dfrac4{4\pi n+3\pi+4i}+\dfrac4{4\pi n+\pi+4i}\right) \ln\dfrac{4n + 3}{4n+1}.\tag{7b}$$
The poly-Stieltjes constants using.
The poly-Stieltjjes constants do not belong to the standard special functions, but they are defined in the Oliver Oloa answer as the known specific functions.
In particular, from $(7b)$ and the given definition in the form of $$\gamma_1(a,b) = \lim\limits_{N\to\infty}\left(\sum\limits_{n=1}^N \dfrac{\ln(n+a)}{n+b} - \dfrac{\ln N^2}2\right)\tag{$\large\diamond$}$$ should $$\begin{align} &I_1= \dfrac{16}{16+9\pi^2}\,\ln3 - \dfrac1\pi \Im\left(\gamma_1\left(\small\dfrac34,\frac34+\frac i\pi\right) - \gamma_1\left(\small\dfrac14,\frac34+\frac i\pi\right) \right)\\[4pt] &-\dfrac{16}{16+\pi^2}\,\ln3 + \dfrac1\pi \Im\left(\gamma_1\left(\small\dfrac34,\frac14+\frac i\pi\right) - \gamma_1\left(\small\dfrac14,\frac14+\frac i\pi\right) \right), \end{align}\tag8$$
$$\begin{align} &I=-\dfrac14\tanh 2\ln\left(\dfrac{\pi^2}4+1\right) + \dfrac{1+\operatorname{sech}2}2 \arctan \,\dfrac\pi2 +\dfrac{64\pi^2}{(16+\pi^2)(16+9\pi^2)}\\[4pt] &+\dfrac1{2\pi}\Im\left(\gamma_1\left(\small\dfrac34,\frac34+\frac i\pi\right) - \gamma_1\left(\small\dfrac14,\frac34+\frac i\pi\right) \right)\\[4pt] &- \dfrac1{2\pi} \Im\left(\gamma_1\left(\small\dfrac34,\frac14+\frac i\pi\right) - \gamma_1\left(\small\dfrac14,\frac14+\frac i\pi\right) \right). \end{align}\tag9$$
Formula $(9)$ gives the closed-form representation, which cannot be used in the popular package Wolfram Alpha.
Results.
corresponds to the numerical calculations of the given integral
.
A good fit for $\frac{1}{1+\tan x}$ in $[0,\frac{\pi}{2}]$ is $1-\frac{2}{\pi}x$
So
$$I_{approx}=\int_0^{\frac{\pi}{2}}\frac{1-\frac{2}{\pi}x}{1+x^2}dx=\arctan \frac{\pi}{2}-\frac{1}{\pi}\ln\left (1+ \frac{\pi^2}{4} \right )$$ Absolute error is about $0.011$
