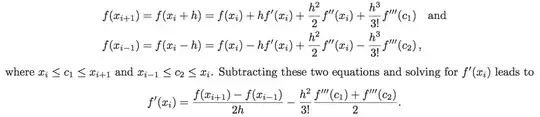I found this visual "proof" of $\oint zdz = 0$ and $\oint dz/z = 2\pi i$ quite compelling and first want to share it with you. But I have a real question, too, which I will ask at the end of this post, so please stay tuned.
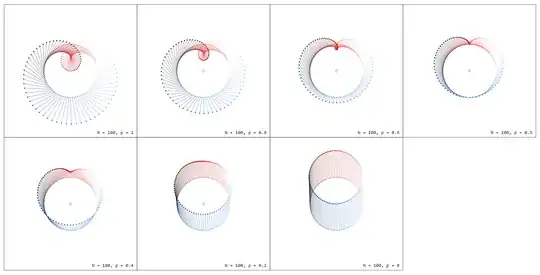
Consider the unit circle $C_1$ in $\mathbb{C}$ with $n$ equally distributed numbers $z_k = e^{i2\pi k/n}$. Draw from each $z_k$ an arrow to $z_k + f(z_k)$ for $f(z) = z$ resp. $f(z) = 1/z$. To make the connection between $z$ and $1/z$ more comprehensible I plot the graphs $f_p(z) = pz + (1-p)/z$ for some values of $0 \leq p \leq 1$. Note that $f_1(z) = z$ and $f_0(z) = 1/z$.
[click image to enlarge]
Note that these plots are essentially stream plots a) restricted to the unit circle and b) displaying not only the direction of the vector field but also its magnitude.
Note that by $f_p(-z) = -f_p(z)$ we have $\sum_{k=0}^{n-1}f_p(z_k) = 0$ for all $p$ which can more easily be seen when drawing $f_p(z)$ from the origin:
Note the difference in color between $f_1(z) = z$ and $f_0(z) = 1/z$ which is due to different phases $\varphi = 2\pi k/n$ of the arguments.
Now let's consider the factor $d_nz$, which is the secant (for $n\rightarrow \infty$ the tangent) vector of the circle at point $z$. Multiplying $f(z)$ by $d_nz$ shrinks and rotates $f(z)$. Because $|d_nz|\rightarrow 0$ for $n\rightarrow\infty$, we would have $|f(z)d_nz| \rightarrow 0$, too, so to keep the vector $f(z)d_nz$ visible, we normalize $d_nz$ by division by $|d_nz| = 2\pi/n$. So, only the rotation of $f(z)$ is in the focus:
Now we are already done: For $f(z) = f_1(z) = z$ the vectors $f(z_k)dz$ still sum up to $0$, while for $f(z) = f_0(z) = 1/z$ we have $n$ vectors of length $1$ all pointing into the same direction (up), so there sum is just $n\cdot i$. Multiplying by the normalization factor $2\pi/n$ we get the desired result:
$$\sum_{k=0}^{n-1}f_0(z_k)d_nz = 2\pi i$$
which holds for arbitrary $n$.
Put algebraically, one finds with $\zeta_k = e^{i2\pi k/n}$ the $n$-th roots of unity, $d_k = \zeta_k e^{i\pi / 2}$, and $1/\zeta_k = \overline{\zeta_k}$:
$$\sum_{k=0}^{n-1}\zeta_k d_k = \sum_{k=0}^{n-1}\zeta_k^2 e^{i\pi / 2} = i \sum_{k=0}^{n-1}\zeta_k^2 = i \sum_{k=0}^{n-1}\zeta_k = 0$$
$$\sum_{k=0}^{n-1}\overline{\zeta_k} d_k = \sum_{k=0}^{n-1}\overline{\zeta_k}\zeta_k e^{i\pi / 2} = i \sum_{k=0}^{n-1}1 = i \cdot n$$
Again, to see this more clearly, we can draw $f(z)d_nz$ from the origin:
Note that the single point for $p=0$, i.e. $f_0(z) = 1/z$, represents in fact $n$ points, all at the same position.
The proof sketched here was somehow "synthetic" or geometrical. It's interesting to compare it with the analytic proof:
$$\oint_{C_1} dz/z = \int _0 ^{2 \pi} \dfrac{i e^{i z}}{e^{i z}} dz = \int _0 ^{2 \pi}i dz = 2 \pi i $$
and the proof by Cauchy's residue theorem
$$\oint_{C_1} dz/z = 2\pi i \operatorname{I}(C_1,0)\operatorname{Res}(1/z,0)= 2 \pi i$$
with $\operatorname{I}(C_1,0) = 1$ the winding number of $C_1$ around $0$ and $\operatorname{Res}(1/z,0) = 1$ the residue of $f(z)=1/z$ at $0$.
What I don't see in the pictures above is, what the value of the integral has to do with the existence of a pole at $0$, so my question is:
By which kind of "long-range interaction" does the singularity at $0$ "force" the vectors $dz/z$ to rotate exactly the way they do, summing up to $2\pi i$?
Addendum 2
Dirk asked for pictures for $f(z) = 1/z^2$. Here they are for $z \rightarrow z + f(z)$, $z \rightarrow z + f(z)d_nz$, , $0 \rightarrow f(z)d_nz$:
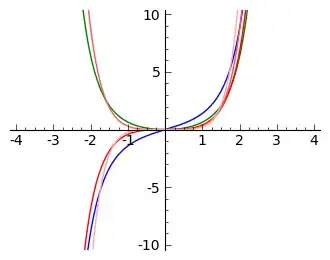
For the sake of comparison here are the plots for $f(z) = z^k$, $k = 1,2,3,4$ (upper rows) and $f(z) = 1/z^k$ (lower rows):
Note the special character of the bottom left plot in the second picture which is the one that relates to the residue of $z^{-1}$ at $z=0$ being $1$. All other residues of $z^{\pm k}$ at $z=0$ are $0$.
Note also how derivation acts as rotation.
Addendum 1
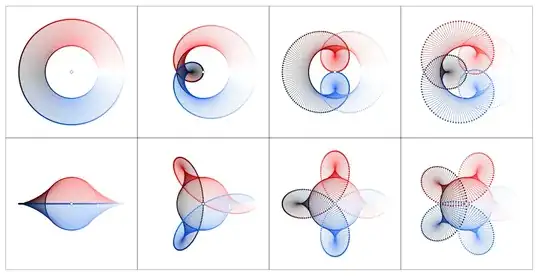
For the sake of comparison: The same visual proof works – even though not so easy to see at a glance – for other closed curves, e.g. a cardioid $\gamma$. In the first table you'll see $z \rightarrow z + f(z)$, in the second $z \rightarrow z + f(z)d_nz$, in the third $0 \rightarrow f(z)d_nz$. With a little experience you will "see" that $\oint_\gamma zdz = 0$ and $\oint_\gamma dz/z = 2\pi i$
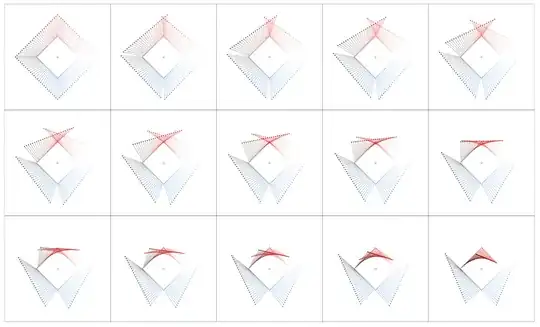
And here for the diamond curve: the tables for $z \rightarrow z + f(z)$, $z \rightarrow z + f(z)d_nz$, and $0 \rightarrow f(z)d_nz$
The rotation of $f(z)$ as induced by multiplication by $dz$ can be seen as a "process" in stop motion:
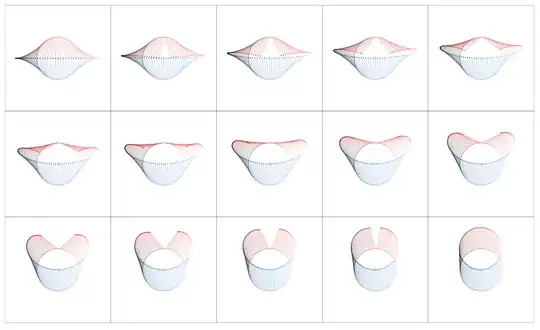Note that in these two cases – based on the circle – $f(0)$ is rotated by $\pi/2$, $f(e^{i\pi/2})$ by $\pi$, $f(e^{i\pi})$ by $-\pi/2$, and $f(e^{i3\pi/2})$ by $0$.
