Why determinant of a 2 by 2 matrix is the area of a parallelogram?

Question

Let $A=\begin{bmatrix}a & b\\ c & d\end{bmatrix}$.

How could we show that $ad-bc$ is the area of a parallelogram with vertices $(0, 0),\ (a, b),\ (c, d),\ (a+b, c+d)$?

Are the areas of the following parallelograms the same?

$(1)$ parallelogram with vertices $(0, 0),\ (a, b),\ (c, d),\ (a+c, b+d)$.

$(2)$ parallelogram with vertices $(0, 0),\ (a, c),\ (b, d),\ (a+b, c+d)$.

$(3)$ parallelogram with vertices $(0, 0),\ (a, b),\ (c, d),\ (a+d, b+c)$.

$(4)$ parallelogram with vertices $(0, 0),\ (a, c),\ (b, d),\ (a+d, b+c)$.

Thank you very much.

Answer 1

Spend a little time with this figure due to Solomon W. Golomb and enlightenment is not far off:

(Appeared in Mathematics Magazine, March 1985.)

Answer 2

I know I'm extremely late with my answer, but there's a pretty straightforward geometrical approach to explaining it. I'm surprised no one has mentioned it. It does have a shortcoming though - it does not explain why area flips the sign, because there's no such thing as negative area in geometry, just like you can't have a negative amount of apples(unless you are economics major).

It's basically:

  Parallelogram = Rectangle - Extra Stuff.

If you simplify $(c+a)(b+d)-2ad-cd-ab$ you will get $ad-bc$.

Also interesting to note that if you swap vectors places then you get a negative(opposite of what $ad-bc$ would produce) area, which is basically:

  -Parallelogram = Rectangle - (2*Rectangle - Extra Stuff)

Or more concretely:

$(c+a)(b+d) - [2*(c+a)(b+d) - (2ad+cd+ab)]$

Also it's $bc-ad$, when simplified.

The sad thing is that there's no good geometrical reason why the sign flips, you will have to turn to linear algebra to understand that.

Like others had noted, determinant is the scale factor of linear transformation, so a negative scale factor indicates a reflection.

Answer 3

The oriented area $A(u,v)$ of the parallelogram spanned by vectors $u,v$ is bilinear (eg. $A(u+v,w)=A(u,w)+A(v,w)$ can be seen by adding and removing a triangle) and skew-symmetric. Hence $A(ae_1+be_2,ce_1+de_2)=(ad-bc)A(e_1,e_2)=ad-bc$. (the same works for oriented volumes in any dimension)

Answer 4

For the matrix $\left[\begin{array}{cc} a & c \\ b & d \\ \end{array}\right]$ let $$A = \left[\begin{array}{c} a \\ b \\ \end{array}\right] \;\text{and}\; B = \left[\begin{array}{c} c \\ d \\ \end{array}\right]$$

as shown in the following figure.

Then the height of the parallelogram is

$$\text{height} = |B|\sin\alpha = |B|\cos\beta.$$

If we rotate $A$ by 90 degrees in the CCW direction as follows:

$$R_{90º}A = \left[\begin{array}{cc} 0 &-1 \\ 1 &0 \\ \end{array}\right] \left[\begin{array}{c} a \\ b \\ \end{array}\right] = \left[\begin{array}{c} -b \\ a \\ \end{array}\right],$$

maintaining the magnitude of the base as

$$\text{base} = |A| = |R_{90º}A|,$$

then it is clear that the area of the parallelogram is therefore

$$ \text{base}\times\text{height}=(|A|)(|B|\sin\alpha) = |R_{90º}A|\;|B|\cos\beta = (R_{90º}A)\cdot B = \left[\begin{array}{c} -b \\ a \\ \end{array}\right] \cdot \left[\begin{array}{c} c \\ d \\ \end{array}\right] = ad-bc. $$ Q.E.D.

Answer 5

I keep forgetting the tricks to prove this so I found the only way to remember it is to stick to basic principles. We can deform the parallelogram to get a square like so.

Now we only need to find the side lengths of this rectangle. The height is easy, it's just d. To get the base length, we find:

and so with a little algebra we find that the base length is $a-b\times\frac{c}{d}$.

Hence the area is just $$ d(a-\frac{bc}{d}) = ad - bc$$

Answer 6

Here is an animated gif I made to derive the area of a parallelogram.

Answer 7

If you compute the cross product of (a,b,0) and (c,d,0), then you get (in the third coordinate) ad-bc. This is, up to the sign, the area of the parallelogram.

BTW I think that (3) and (4) are not parallelograms, are they?

Answer 8

Also, if the coordinates of any shape are transformed by a matrix, the area will be changed by a scale factor equal to the determinant.

Since the determinant is the scale factor when the unit square is transformed to a parallelogram, it will be the scale factor when any parallelogram with the origin as a vertex is transformed to any other parallelogram because the inverse matrix will transform a parallelogram back into a square and has reciprocal determinant. If there is no inverse, the determinant is 0 and the transformed shape has no area.

Any triangle with the origin as a vertex can be drawn as half of a parallelgram including the origin. Any triangle not including the origin is the area of a triangle containing the origin minus two triangles inside not containing the origin. The area of any shape can be split into triangles, although an infinite number will be required if it has curved sides.

Answer 9

Wrote this for a linear algebra class of mine. The argument is predicated on using shears.

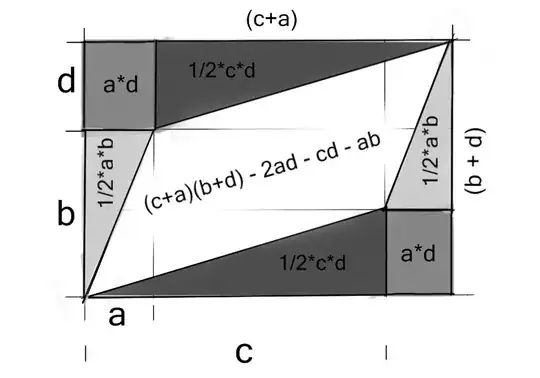
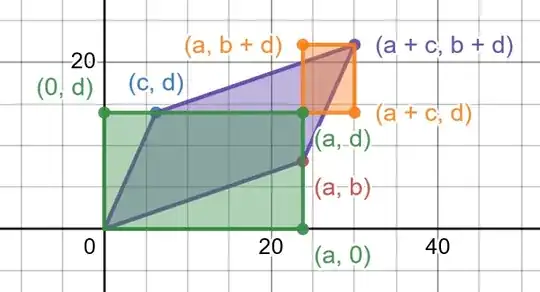
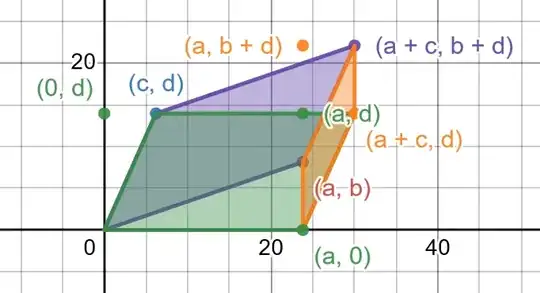
Assume you have two vectors, (a, ay) and (xd, xyd+d). Weird choice and abundance of variables to be explained in a moment. I can obviously find the determinant of this, which is ad (do it).

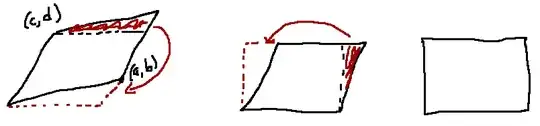
So if I want to prove that the determinant is an area, I need to show that these weirdo vectors share an area with (a,0) and (0,d), which also has the determinant ad. Well, it turns out what I can do is shear the matrix with (a,0) and (0,d) as columns, since a shear does not alter the area at all (show this geometrically).

Take vector (a,0) and (0,d) and apply shear matrix (1,x,0,1), followed by (1,0,y,1), which gives you the original weirdo vectors (a,ay) and (xd, xyd+d). Since the shears do not change area, and we know the area of the rectangle formed by (a,0) and (0,d), the area of two arbitrary vectors may be expressed by its determinant, which we have shown to be identical to the determinant of rectangular matrix (a,0,0,d). QED.

You can extend this argument to 3D, etc. by applying shears in any arbitrary direction. Therefore, a determinant will provide you with a volume in any R^n.

Answer 10

I made the following slide to explain where this formula comes from:

Answer 11

Another geometric proof using an animation in desmos:

The green rectangle and parallelogram have the same base and height:

$\operatorname{green}=\operatorname{area}\left((0,0)(a,0)(a,d)(0,d)\right)=ad= \operatorname{area}\left((0,0)(a,0)(a,{c}+d)(c,d)\right).$

The orange rectangle and parallelogram have the same base and height:

$\operatorname{orange}=\operatorname{area}\left((a,d)(a+c,d)(a+c,b+d)(a,b+d)\right)=bc= \operatorname{area}\left((a,0)(a+c,d)(a+c,b+d)(a,b)\right).$

The violet, green and orange parallelograms have the same bases, the height of green parallelogram is the sum of heights of violet and orange parallelograms.

$\operatorname{violet} + \operatorname{orange} = \operatorname{green}$

$\operatorname{violet}=\operatorname{area}\left((0,0)(a,b)(a+c,b+d)(c,d)\right) = \operatorname{green} - \operatorname{orange} = ad-bc$