Recursive Integration over Piecewise Polynomials: Closed form?

Question

Is there a closed form to the following recursive integration?

$$ f_0(x) = \begin{cases} 1/2 & |x|<1 \\ 0 & |x|\geq1 \end{cases} \\ f_n(x) = 2\int_{-1}^x(f_{n-1}(2t+1)-f_{n-1}(2t-1))\mathrm{d}t $$ It's very clear that this converges against some function and that quite rapidly, as seen in this image, showing the first 8 terms:

Furthermore, the derivatives of it have some very special properties.
Note how the (renormalized) derivatives consist of repeated and rescaled functions of the previous degree which is obviously a result of the definition of the recursive integral:

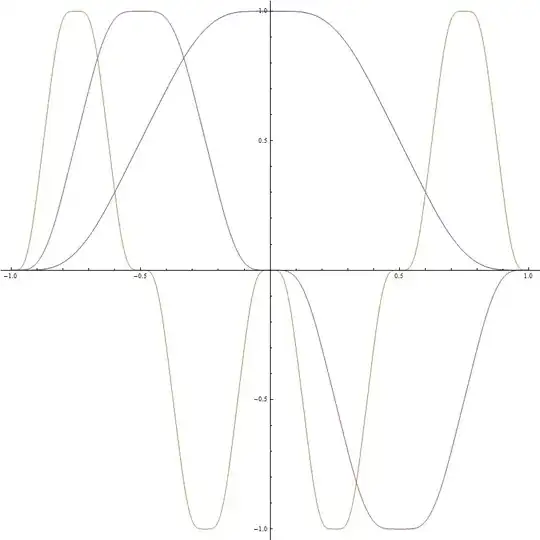
EDIT
I found the following likely Fourier transform of the expression above. I do not have a formal proof but it holds for all terms I tried it with (first 11). $$ \mathcal{F}_x\left[f_n(x)\right](t)=\frac{\sin \left(2^{-n} t\right) \left(\prod _{k=1}^n \frac{2^{k+1} \sin \left(2^{-k} t\right)}{t}\right)}{\sqrt{2 \pi } t}$$

Here an image of how that looks like (first 10 terms in Interval $[-8\pi,8\pi]$):

With this, my question alternatively becomes:
What, if there is one, is the closed form inverse fourier transform of

$\mathcal{F}_x\left[f_n(x)\right](t)=\frac{\sin \left(2^{-n} t\right) \left(\prod _{k=1}^n \frac{2^{k+1} \sin \left(2^{-k} t\right)}{t}\right)}{\sqrt{2 \pi } t}$,
especially for the case $n\rightarrow\infty$?

Answer 1

Here is a formula for $f_n$:

\[ f_n(x) = \sum_{j=0}^{2^n} \left( \frac{c_n(j) - c_n(j-1)}{2}\frac{\left(2^n x + 2^n - 2j\right)^n H\left(2^nx + 2^n - 2j\right)} {n!2^{n(n-1)/2}} \right). \]

Here $H$ is the Heaviside step function, $c_n$ is defined by \[ c_n(j) = \begin{cases} 0 & \text{if $j<0$}\\ (-1)^{s(j)} & \text{if $0\leq j < 2^n$} \\ 0 & \text{if $j\geq 2^n$} \end{cases} \] and $s(j)$ is the sum of the digits of the binary representation of $j$. (For example $s(13) = s(0\text{b}1101) = 3$.)

While the Heaviside function is crucial to deriving the formula, it can be removed from the final result using the floor function (denoted $\lfloor \cdot \rfloor$):

\[ f_n(x) = \sum_{j=0}^{\lfloor2^{n-1}(x+1)\rfloor} \left( \frac{c_n(j) - c_n(j-1)}{2}\frac{\left(2^n x + 2^n - 2j\right)^n} {n!2^{n(n-1)/2}} \right). \]

Here is a plot of $f_{15}$ using this formula:

Deriving the formula

First, separate the definition into two integrals and change variables, $2t+1 \mapsto t$ in the first, and $2t-1\mapsto t$ in the second, giving

\[ f_{n+1}(x) = \int_{-1}^{2x+1} f_n(t)\ dt - \int_{-3}^{2x-1}f_n(t)\ dt \]

Of course, we can change the -3 to -1 and combine these to a single integral:

\[ f_{n+1}(x) = \int_{2x-1}^{2x+1} f_n(t)\ dt \]

Then rewrite $f_0=(1/2)(H(t+1) - H(t-1))$. Note that the integral of $H(t)$ is $tH(t)$, whose integral is $(t^2/2)H(t)$, and so forth. Now we can write $f_n$ as a single iterated integral, for example

\[ f_3(x) = \frac12 \int_{2x-1}^{2x+1} \int_{2y-1}^{2y+1} \int_{2z-1}^{2z+1} (H(t-1) - H(t+1))dt\ dz\ dy \]

Each integration can be done doing several different changes of variables. This gives rise to the powers of 2 in the denominator.

Notes

Each $f_n$ is symmetric. The part from -1 to -0.5 is repeated four times. Due to the way that Heaviside functions work, it is computationally easiest to compute values for $f_n(x)$ for $x$ closer to -1.

Code

Here is some Python code to compute $f_n(x)$.

from __future__ import division
from math import factorial

def c(j, n):
    if j < 0 or j >= 2**n:
        return 0
    else:
        return (-1)**bin(j).count("1")

def f(x, n):
    numerator = 0
    for j in xrange(int(2**(n-1) * (x+1))):
        numerator += (c(j, n) - c(j-1, n)) * (2**n * x + 2**n - 2*j)**n
    denominator = 2 * 2**(n*(n-1)/2) * factorial(n)
    return numerator/denominator

print f(-0.75, 10)

Answer 2

Suppose $f$ is a fixed point of the iterations. Then $$f(x) = 2\int_{-1}^x\big(f(2t+1)-f(2t-1)\big)\,\mathrm{d}t,$$ which, upon differentiating both sides by $x$, implies that $$f'(x) = 2\big(f(2x+1)-f(2x-1)\big).$$ I'll assume that $f$ vanishes outside $[-1,1]$, which you can presumably prove from the initial conditions. Then we get $$f'(x) = \begin{cases} 2f(2x+1) & \text{if }x\le0, \\ -2f(2x-1) & \text{if }x>0. \end{cases}$$ This is pretty close to the definition of the Fabius function. In fact, your function would be $\frac{\text{Fb}'(\frac{x}{2}+1)}{2}$

The Fabius function is smooth but nowhere analytic, so there isn't going to be a nice closed form for your function.

Answer 3

This equation \begin{equation}f'(x)=2f(2x+1)-2f(2x-1), \quad f(0) = 1, \tag{$*$} \end{equation} has a finite solution which is also known as the $\mathrm{up}(x)$ or $\mathrm{hut}(x)$ function. It has compact support $\mathrm{supp}\,\mathrm{{up}}(x)=[-1,1]$ and its Fourier transform is $\hat{f}(t)=\prod\limits_{k=1}^{\infty}\mathrm{sinc}{(t\cdot 2^{-k})}.$ So, $\mathrm{up}(x)$ is defined by inverse Fourier transform as follows $$ \mathrm{up}(x)=\frac{1}{2\pi}\int\limits_{\mathbb{R}}e^{-itx}\hat{f}(t)\,dt= \frac{1}{2\pi}\int\limits_{\mathbb{R}}e^{-itx}\prod\limits_{k=1}^{\infty}\mathrm{sinc}{(t\cdot 2^{-k})}\,dt. $$

Equation $(*)$ and its finite solution $\mathrm{up}(x)$ was independently introduced in 1971 by V.L. Rvachev, V.A. Rvachev and W. Hilberg. It's interesting to note that a simpler version of $(*)$ was introduced by J. Fabius only 5 years earlier: \begin{equation}f'(x)=2f(2x), \quad f(0) = 0. \tag{$**$} \end{equation} By the way, the signs of the first 2 derivatives of $\mathrm{up}(x)$ are the elements of Thue-Morse sequence $\{+1,-1,-1,+1\}$ as well.

P.S. I've uploaded some plots here of generalizations of $\mathrm{up}(x)$ which is known as the $\mathrm{h}_a(x)$ function.