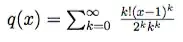88

Can rotations and translations of this shape

enter image description here

perfectly tile some equilateral triangle?

I've now also asked this question on mathoverflow.

Notes:

  • Obviously I'm ignoring the triangle of side $0$.
  • Because the area of the triangle has to be a multiple of the area of the tile, the triangle must have side length divisible by $5$ (where $1$ is the length of the short edges of the tile).
  • The analogous tile made of three equilateral triangles can tile any equilateral triangle with side length divisible by three.
  • There is a computer program, Burr Tools, which was designed to solve this kind of problem. Josh B. has used it to prove by exhaustive search that there is no solution when the side length of the triangle is $5$, $10$, $15$, $20$ or $25$. Lengths of $30$ or more will take a very long time to check.
  • This kind of problem can often be solved be a colouring argument but I've failed to find a suitable colouring. (See below.)
  • Lee Mosher pointed me in the direction of Conway's theory of tiling groups. This theory can be used to show that if the tile can cover an equilateral triangle of side length $n$ then $a^nb^nc^n=e$ in the group $\left<a,b,c\;\middle|\;a^3ba^{-2}c=a^{-3}b^{-1}a^2c^{-1}=b^3cb^{-2}a=b^{-3}c^{-1}b^2a^{-1}=c^3ac^{-2}b=c^{-3}a^{-1}c^2b^{-1}=e\right>$. But sadly it turns out that we do have that $a^nb^nc^n=e$ in this group whenever $n$ divides by $5$.
  • In fact one can use the methods in this paper of Michael Reid to prove that this tile's homotopy group is the cyclic group with $5$ elements. I think this means that the only thing these group theoretic methods can tell us is a fact we already knew: that the side length must be divisible by $5$.
  • These group theoretic methods are also supposed to subsume all possible colouring arguments, which means that any proof based purely on colouring is probably futile.
  • The smallest area that can be left uncovered when trying to cover a triangle of side length $(1,\dots,20)$ is $($$1$$,\,$$4$$,\,$$4$$,\,$$1$$,\,$$5$$,\,$$6$$,\,$$4$$,\,$$4$$,\,$$6$$,\,$$5$$,\,$$6$$,\,$$4$$,\,$$4$$,\,$$6$$,\,$$5$$,\,$$6$$,\,$$4$$,\,$$4$$,\,$$6$$,\,$$5$$)$ small triangles. In particular it's surprising that when the area is $1\;\mathrm{mod}\;5$ one must sometimes leave six triangles uncovered rather than just one.
  • We can look for "near misses" in which all but $5$ of the small triangles are covered and in which $4$ of the missing small triangles could be covered by the same tile. There's essentially only one near miss for the triangle of side $5$, none for the triangle of side $10$ and six (1,2,3,4,5,6) for the triangle of side $15$. (All other near misses can be generated from these by rotation, reflection, and by reorienting the three tiles that go around the lonesome missing triangle.) This set of six near misses are very interesting since the positions of the single triangle and the place where it "should" go are very constrained.
Oscar Cunningham
  • 15,389
  • 3
  • 43
  • 77
  • 2
    Conway's Tiling Groups might be relevant; see Thurston's article http://www.cimat.mx/ciencia_para_jovenes/pensamiento_matematico/thurston.pdf. It might be fun to work out. – Lee Mosher Apr 03 '17 at 15:42
  • @LeeMosher Thanks! I read the paper, and what it says in this case is that a necessary condition for the existence of a tiling on a triangle of side $n$ is that $a^{-n}b^nc^{-n}=e$ in the group $\left$ (the six relations correspond to the six possible orientations of the tile). I have no idea how to solve this kind of problem, but I'll look into it. So far the only information I've coaxed out of GAP is that the group is infinite. – Oscar Cunningham Apr 03 '17 at 19:17
  • That agrees with what I understand of this problem, I worked out the relations similarly to how you did. But yeah, conceivably it is still a hard group theory problem. – Lee Mosher Apr 03 '17 at 20:28
  • By the way, I suggest adding the group theory tag, if you want to attract some interest to this question. But you would have to remove one of your other tags because you are maxxed out at 5 tags at the moment. – Lee Mosher Apr 03 '17 at 20:31
  • 3
    @LeeMosher I'll kick out [recreational-mathematics]. This is now serious business! :-) – Oscar Cunningham Apr 03 '17 at 21:05
  • @LeeMosher No luck, it turns out that $a^{-n}b^nc^{-n}$ really is the identity when $n$ divides by $5$. – Oscar Cunningham Apr 04 '17 at 06:51
  • 1
    Ho ho, that's interesting. I believe section 4 of the Thurston article gives some ideas of how to use the tiling group to actually produce a tiling when you suspect one might exist, although my guess is that it is a more ad hoc method. – Lee Mosher Apr 04 '17 at 12:24
  • 3
    I used BurrTools to determine there is no tiling for a triangle of width 25. This took 21 hours on my computer. I'm not going to try width 30. – Josh B. Apr 04 '17 at 20:55
  • @JoshB. Thanks! I didn't know about BurrTools. I had been using [this](https://github.com/blynn/dlx) solver for the exact cover problem but it had been running for a couple of days on the length $25$ case without success. I just downloaded BurrTools and it's much faster. – Oscar Cunningham Apr 05 '17 at 10:02
  • Does this shape tile *any* triangle? – preferred_anon Apr 05 '17 at 10:34
  • @DanielLittlewood If it tiles a triangle then that triangle must be equilateral, since in order for the tile to fit into the corners the angles must be a multiple of $60^\circ$. – Oscar Cunningham Apr 05 '17 at 10:36
  • @OscarCunningham Fair enough! – preferred_anon Apr 05 '17 at 10:37
  • 3
    A couple close calls: [one](http://i.imgur.com/NOaHCN9.png) [two](http://i.imgur.com/srFDyRm.png) – Josh B. Apr 07 '17 at 00:23
  • @JoshB. Wow, cool. Here's something else interesting: I've had Burr Tools looking for tilings of rhombuses and it seems like all of them use only four of the six possible orientations. In particular they don't use the two orientations where the strip runs parallel to the short diagonal. If we could prove that they never used these orientations then we'd be done since if we could tile a triangle then we could stick two such triangles together to make a tiling of a rhombus with at least a third of the tiles in one of those orientations. – Oscar Cunningham Apr 07 '17 at 15:48
  • 4
    @OscarCunningham You can fill a rhombus with these pieces in all orientations. [example](http://i.imgur.com/0Qb3tOC.png) Still, it seems that the orientations you point out do dominate the tiling. However, I'm not convinced this will remain the case as we examine larger rhombuses or triangles. But that's what I find interesting about this problem: my intuition isn't strongly pointing for or against. – Josh B. Apr 07 '17 at 18:13
  • @JoshB. Thank you for pointing that out! I got lazy and missed it. I was thinking that we could graph the side length of the rhombus against the largest achievable fraction of the tiles which are oriented that way. Then we could eyeball whether that fraction would ever rise above a $1/3$ and try to estimate when that would happen. But I think that Burr Tools will take too long to list all the tilings even in the side length $15$ case. – Oscar Cunningham Apr 07 '17 at 18:24
  • [1]: https://i.stack.imgur.com/Uv9PB.gif Does this answer your question? – bio Apr 08 '17 at 00:59
  • @bio Those tiles are shorter than the ones in the question about. They're formed of three small equilateral triangles rather than five. – Oscar Cunningham Apr 08 '17 at 11:07
  • 1
    If a tiling with rows of 5 triangles requires trilateral symmetry, then the side of the big triangle will have to be a multiple of 15. That is because only triangles with a side divisible by 3 have a midpoint not inside one of the tiling triangles. – Χpẘ Apr 09 '17 at 02:41
  • @user2460798 If there is a tiling with trilateral symmetry then there also exists one without trilateral symmetry, since the original tiling can be used four times to cover a triangle with twice the side length, and this can be done in a way that guarantees non-symmetry. – Oscar Cunningham Apr 09 '17 at 16:59
  • @OscarCunningham I don't get how a tiling of 4 triangles isn't trilaterrally symmetric. You can rotate the large triangle $2\pi/3$ three times and get the same image. (There's only one way to tile an equilateral triangle with 4 triangles whose side is half the length). – Χpẘ Apr 09 '17 at 19:26
  • @user2460798 You break the symmetry by replacing one of the small triangles (not the one in the centre) with its reflection. – Oscar Cunningham Apr 09 '17 at 19:33
  • I just started Burr tools with side length 30. It says the search will be finished in 10 years.... – didgogns Apr 11 '17 at 12:31
  • I found some things about the solution: If length of a big equilateral triangle is $n$, then $n=5m^2$. Also $m>1$ is odd number. Therefore $n\in \{ 45, 125, \dots \}$. Minimum possible value of $n$ is $45$. But I didn't find suitable tile for $n=45$. I didn't use any calculating program, only pencil and paper. If you want see my partial solution, I can send it. – scarface Apr 11 '17 at 23:35
  • @scarface Yes, please submit that as an answer! – Oscar Cunningham Apr 11 '17 at 23:43
  • @scarface On second thoughts, I suspect you've made a mistake. If you can tile a triangle of side $5m^2$ then you should also be able to tile a triangle of side $10m^2$ by using four copies of your original tiling. Since $10m^2$ is never equal to $5{m'}^2$ you've either made a mistake or you've proved that there can't be any tiling at all! – Oscar Cunningham Apr 12 '17 at 00:31
  • Yeah, I made a mistake in proof of $m$. $m$ may be even. I will sent ... – scarface Apr 12 '17 at 00:53
  • @scarface How do you get $n=5m^2$? Shouldn't it be $n^2=5m$ where $m$ is the number of pieces used in the tiling. – Josh B. Apr 12 '17 at 01:11
  • 1
    Sorry, I didn' find anything. Lengt of a side of the big equilateral triangle is $n$. Therefore we have $n^2$ times unit equilateral triangles. In the figure, $k$-th row has $2k-1$ unit equilateral triangles. Let's paint with red color to $k$ times unit triangles and paint with white color to $k-1$ times unit triangles, in $k$-th row. [![enter image description here][1]][1] [1]: https://i.stack.imgur.com/bmG8S.png $x$ times part has $3$ red, $2$ white triangle. $y$ times part has $2$ red, $3$ white triangle. – scarface Apr 12 '17 at 01:39
  • 1
    ... Number of all red triangles $$ 1+2+3+\cdots +n =\dfrac{n(n+1)}{2} $$ and number of all white triangles $$ 1+2+3+\cdots + (n-1) =\dfrac{n(n-1)}{2} $$ Hence, \begin{array}{lcl} 3x+2y & = & \dfrac{n(n+1)}{2} \\ 2x+3y & = & \dfrac{n(n-1)}{2} \end{array} By adding these $5(x+y)=n^2$, $x+y=\dfrac{n^2}5$ and $5 \mid n$. Also we find that $x=\dfrac{n(n+5)}{10} $. But, these are not new things. – scarface Apr 12 '17 at 01:41
  • 1
    If we fix an 'upright' orientation of the triangle there are 6 possible orientations of the tile. Three orientations contain three Δ up triangles while three contain three ∇ down triangles. Thus any tiling must contain $n$ more tiles of the first type then the second where $n$ is the side length. – Daniel Pietrobon Apr 12 '17 at 03:37
  • 2
    I just asked this question on [mathoverflow](https://mathoverflow.net/questions/267095/can-a-row-of-five-equilateral-triangles-tile-a-big-equilateral-triangle). – Oscar Cunningham Apr 13 '17 at 11:14
  • One idea: select a different shape which does tile a triangle, then tile that shape with our $5$ triangle trapezoid. – Josh B. Apr 13 '17 at 21:08

4 Answers4

34

I suppose I should post: I solved this on MathOverflow. The answer is YES: a size-45 triangle can be tiled.

I thank two insights from Josh B here: first that a rhombus with side length 15 can be tiled, and second the strategy to "select a different shape which does tile a triangle, then tile that shape with our $5$ triangle trapezoid."

This $15-15-15-30$ trapezoid can be tiled, and three such trapezoids can tile a triangle with side length $45$.

enter image description here

Oscar Cunningham
  • 15,389
  • 3
  • 43
  • 77
Lopsy
  • 4,513
  • 19
  • 26
  • 1
    Thanks to you! How did you find that tiling? In the MathOverflow post you mention an SAT solver. Any more details? I had attempted this very search with BurrTools but it was going to take far too long. I think BurrTools gets in trouble when there are many ways to tile a subset of the full shape. For example, a rhombus of side length 5 can be tiled in two different ways. A parallelogram of lengths 5 and 6 can be tiled 4 ways. It only gets worse from there. – Josh B. Apr 17 '17 at 01:57
  • Thanks again. I added a picture of the solution to your answer because math.stackexchange answers are supposed to be self-contained. – Oscar Cunningham Apr 17 '17 at 07:06
  • Wonderful solution. Very entertaining how you reduced the problem to the case of three equilateral triangles. – Daniel Pietrobon Apr 17 '17 at 08:58
  • 1
    @Josh B. Nothing special: I had one True/False variable for each possible tile placement, with the constraints "every triangle must be filled" and "any two overlapping tiles can't both exist." I wonder what techniques Burr Tools uses under the hood. An off-the-shelf SAT solver (pycosat) solved this in ~20 seconds, but would take a long time to solve a side-length-25 equilateral triangle. I'm guessing the limited width of the shape helps. – Lopsy Apr 17 '17 at 15:57
  • 1
    It's a rep-tile. The above tiling can be extended with a side-15 rhombus to get a tiling of the original shape using 1125 tiles. – nickgard Apr 19 '17 at 07:56
  • Cool. Could you post the source code? – Mikhail V May 09 '17 at 19:08
  • @MikhailV I've deleted the source code by now, but if it helps, it makes a SAT formula with one Boolean variable per possible trapezoid placement. The constraints are "no two trapezoids overlap" and "every triangle contains at least one trapezoid". – Lopsy May 11 '17 at 14:42
18

Here's the minimal solution, a side-30 triangle. Also posted to MathOverflow here https://mathoverflow.net/questions/267095/can-a-row-of-five-equilateral-triangles-tile-a-big-equilateral-triangle.enter image description here

theonetruepath
  • 443
  • 3
  • 7
3

Some people were interested in heptiamond tiling. I found that the shortest trapezoid that can be tiled has 15 rows.

enter image description here (click for larger image)

I think that this trapezoid plus parallelograms are sufficient to tile an equilateral triangle. [Edit: Nevermind, see "Tiling a triangle" below]

How I found this:

We start with an empty trapezoid, with 15 rows, and add heptiamonds left-to-right one at a time. We can only add a heptiamond if it doesn't leave a "gap" in any row. This way, we can represent our current state with only one number per row: the number of triangles in it.

enter image description here

Implicitly, our rows start with some triangles already. The bottom row has 1 triangle, the next row up has 3 triangles, then 5, 7, 9, ...

Also, we only need to keep track of the number of triangles in each row modulo 7, since we can always add a "flat" heptiamond, affecting only a single row.

So our state space has size 7^15 (~4.7 trillion).

From the starting configuration of {1,3,5,0,2,4,6,1,3,5,0,2,4,6,1} we do a breadth-first search and reach {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1} -- meaning that each row has the same number of triangles (modulo 7).

Here is the progression of states corresponding to adding one yellow heptiamond at a time:

{1,3,5,0,2,4,6,1,3,5,0,2,4,6,1}
{1,5,0,2,3,4,6,1,3,5,0,2,4,6,1}
{1,5,0,2,4,6,1,3,3,5,0,2,4,6,1}
{1,0,2,4,5,6,1,3,3,5,0,2,4,6,1}
{1,0,2,4,6,1,3,5,3,5,0,2,4,6,1}
{1,2,4,6,0,1,3,5,3,5,0,2,4,6,1}
{1,2,4,6,1,3,5,0,3,5,0,2,4,6,1}
...
{1,1,1,1,1,1,1,1,2,2,2,2,2,2,2}
{1,1,1,1,1,1,1,1,2,2,2,3,4,4,4}
{1,1,1,1,1,1,1,1,4,4,4,4,4,4,4}
{1,1,1,1,1,1,1,1,4,4,4,5,6,6,6}
{1,1,1,1,1,1,1,1,6,6,6,6,6,6,6}
{1,1,1,1,1,1,1,1,6,6,6,0,1,1,1}
{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}

Note that each state changes exactly 4 adjacent rows. For example, the first change is {3,5,0,2} -> {5,0,2,3}. There are only 28 such transitions possible, corresponding to the 4 non-flat heptiamond orientations, at 7 possible offsets each.

Pentiamond:

The pentiamond requires 8 rows

enter image description here

Tiling a triangle:

Initially, I thought a 15-row trapezoid would be useful for tiling a triangle, but my initial idea didn't work. Instead, I found a 21-row trapezoid: enter image description here

This was found by doing a similar search, but switching the search space to consider only the first 15 rows. Except, when the first 6 rows are "0", only the last 15 rows are considered. (With this trick, my program could run within my machine's 16GB of memory).

enter image description here

These trapezoids can be stacked and padded to tile a 1-1-1-2 ratio trapezoid. 3 of these mega-trapezoids tile an equilateral triangle.

Note that it's important for the trapezoid to have 21 rows (a multiple of 7) instead of 15 rows. Then the trapezoid can be "extended" by any integer length, by appending 21x1 parallelograms.

Tom Sirgedas
  • 536
  • 5
  • 7
3

SAT-solver (glucose) + requiring rotational symmetry very quickly finds solutions for side-30. For example:

enter image description here

Without requiring symmetry, glucose took ~1 hour to find a solution. (Note that rotational symmetry requires side-length to be a multiple of 3 -- otherwise there is a central triangle).

I didn't have much luck with heptiamonds. But, glucose reported side-49 or fewer is impossible (no symmetry requirement).

Tom Sirgedas
  • 536
  • 5
  • 7