Let's define a sequence of numbers between 0 and 1. The first term, $r_1$ will be chosen uniformly randomly from $(0, 1)$, but now we iterate this process choosing $r_2$ from $(0, r_1)$, and so on, so $r_3\in(0, r_2)$, $r_4\in(0, r_3)$... The set of all possible sequences generated this way contains the sequence of the reciprocals of all natural numbers, which sum diverges; but it also contains all geometric sequences in which all terms are less than 1, and they all have convergent sums. The question is: does $\sum_{n=1}^{\infty} r_n$ converge in general? (I think this is called almost sure convergence?) If so, what is the distribution of the limits of all convergent series from this family?
- 103
- 2
- 6
- 2,505
- 1
- 12
- 26
-
3Not sure if my question itself makes sense: But how about a modified question where `r1` is chosen uniformly randomly from (-1,+1) and we iterate by choosing `r2` from `(-1 x abs(r1),+1 x abs(r1))` Would that series converge too? – curious_cat Feb 05 '17 at 17:24
-
2Your second series almost surely converges absolutely (i. e. $|r_1| + $|r_2|$ + \cdots$ converges) if and only if your first series almost surely converges. Combining that with Byron Schmuland's answer, the modified series almost surely converges absolutely, and so _a fortiori_ almost surely converges. – Michael Lugo Feb 05 '17 at 18:11
4 Answers
Let $(u_i)$ be a sequence of i.i.d. uniform(0,1) random variables. Then the sum you are interested in can be expressed as $$S_n=u_1+u_1u_2+u_1u_2u_3+\cdots +u_1u_2u_3\cdots u_n.$$ The sequence $(S_n)$ is non-decreasing and certainly converges, possibly to $+\infty$.
On the other hand, taking expectations gives $$E(S_n)={1\over 2}+{1\over 2^2}+{1\over 2^3}+\cdots +{1\over 2^n},$$ so $\lim_n E(S_n)=1.$ Now by Fatou's lemma, $$E(S_\infty)\leq \liminf_n E(S_n)=1,$$ so that $S_\infty$ has finite expectation and so is finite almost surely.
-
Wow, really cool! Many thanks, Byron Schmuland! I'd love to know that distribution and the "most probable value" (maybe 1??). I think tomorrow I'll be writing some simulations... – Carlos Toscano-Ochoa Feb 05 '17 at 16:10
-
-
2@ByronSchmuland $S_\infty$ will have the same distribution as $X(1+S_\infty)$ where $X$ is uniformly distributed from 0 to 1. Since that is a recursive expression it does not directly tell you the distribution, but it can be used to sanity check any distribution you came up with. – kasperd Feb 05 '17 at 18:35
-
13...And the distribution of $S_\infty$ is uniquely determined by its Laplace transform $$L(s)=E(e^{-sS_\infty})$$ which is the unique solution of the differential equation $$\left(sL(s)\right)'=e^{-s}L(s)\qquad L(0)=1$$ solved by $$L(s)=\exp\left(-\int_0^s\frac{1-e^{-t}}tdt\right)=\exp\left(-\int_0^se^{-t}\ln\left(\frac{s}t\right)dt\right)$$ – Did Feb 05 '17 at 19:45
-
I am having trouble understanding this. But it looks like every other one has understood it. So it is better to just move on and avoid looking dumb (oh I wish it didn't end this way!) – polfosol Feb 06 '17 at 07:21
-
2@polfosol if your previously drawn number is $a$, a uniformly distributed number between $a$ and $0$ is $a \cdot u$, where $u$ is uniformly distributed between $0$ and $1$. The rest follows by recurrence ($u_1=u$, $u_2 = u_1 \cdot u$...) – Davidmh Feb 06 '17 at 16:21
-
3
-
5@zakoda i.i.d. means "independent identical distribution". Uniform is specifically what kind of distribution (a uniform one where the probability density function is constant over the whole range). – Kyle Feb 07 '17 at 16:18
-
A simple consequence is that $E[S_\infty]=E[u_1(1+u_2+u_2 u_3+\ldots)]=E[u_1](1+E[S_\infty])=1/2+1/2E[S_\infty],$ so $E[S_\infty]=1$. – mjqxxxx Feb 07 '17 at 20:21
-
The probability $f(x)$ that the result is $\in(x,x+dx)$ is given by $$f(x) = \exp(-\gamma)\rho(x)$$ where $\rho$ is the Dickman function as @Hurkyl pointed out below. This follows from the the delay differential equation for $f$, $$f^\prime(x) = -\frac{f(x-1)}{x}$$ with the conditions $$f(x) = f(1) \;\rm{for}\; 0\le x \le1 \;\rm{and}$$ $$\int\limits_0^\infty f(x) = 1.$$ Derivation follows
From the other answers, it looks like the probability is flat for the results less than 1. Let us prove this first.
Define $P(x,y)$ to be the probability that the final result lies in $(x,x+dx)$ if the first random number is chosen from the range $[0,y]$. What we want to find is $f(x) = P(x,1)$.
Note that if the random range is changed to $[0,ay]$ the probability distribution gets stretched horizontally by $a$ (which means it has to compress vertically by $a$ as well). Hence $$P(x,y) = aP(ax,ay).$$
We will use this to find $f(x)$ for $x<1$.
Note that if the first number chosen is greater than x we can never get a sum less than or equal to x. Hence $f(x)$ is equal to the probability that the first number chosen is less than or equal to $x$ multiplied by the probability for the random range $[0,x]$. That is, $$f(x) = P(x,1) = p(r_1<x)P(x,x)$$
But $p(r_1<x)$ is just $x$ and $P(x,x) = \frac{1}{x}P(1,1)$ as found above. Hence $$f(x) = f(1).$$
The probability that the result is $x$ is constant for $x<1$.
Using this, we can now iteratively build up the probabilities for $x>1$ in terms of $f(1)$.
First, note that when $x>1$ we have $$f(x) = P(x,1) = \int\limits_0^1 P(x-z,z) dz$$ We apply the compression again to obtain $$f(x) = \int\limits_0^1 \frac{1}{z} f(\frac{x}{z}-1) dz$$ Setting $\frac{x}{z}-1=t$, we get $$f(x) = \int\limits_{x-1}^\infty \frac{f(t)}{t+1} dt$$ This gives us the differential equation $$\frac{df(x)}{dx} = -\frac{f(x-1)}{x}$$ Since we know that $f(x)$ is a constant for $x<1$, this is enough to solve the differential equation numerically for $x>1$, modulo the constant (which can be retrieved by integration in the end). Unfortunately, the solution is essentially piecewise from $n$ to $n+1$ and it is impossible to find a single function that works everywhere.
For example when $x\in[1,2]$, $$f(x) = f(1) \left[1-\log(x)\right]$$
But the expression gets really ugly even for $x \in[2,3]$, requiring the logarithmic integral function $\rm{Li}$.
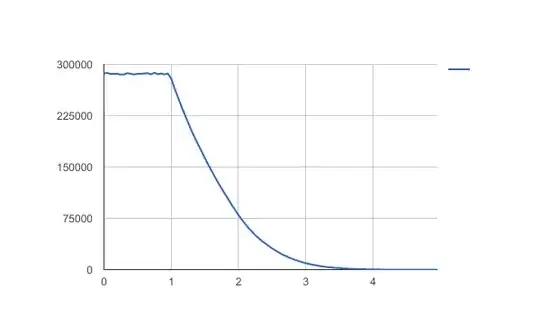
Finally, as a sanity check, let us compare the random simulation results with $f(x)$ found using numerical integration. The probabilities have been normalised so that $f(0) = 1$.
The match is near perfect. In particular, note how the analytical formula matches the numerical one exactly in the range $[1,2]$.
Though we don't have a general analytic expression for $f(x)$, the differential equation can be used to show that the expectation value of $x$ is 1.
Finally, note that the delay differential equation above is the same as that of the Dickman function $\rho(x)$ and hence $f(x) = c \rho(x)$. Its properties have been studied. For example the Laplace transform of the Dickman function is given by $$\mathcal L \rho(s) = \exp\left[\gamma-\rm{Ein}(s)\right].$$ This gives $$\int_0^\infty \rho(x) dx = \exp(\gamma).$$ Since we want $\int_0^\infty f(x) dx = 1,$ we obtain $$f(1) = \exp(-\gamma) \rho(1) = \exp(-\gamma) \approx 0.56145\ldots$$ That is, $$f(x) = \exp(-\gamma) \rho(x).$$ This completes the description of $f$.
- 1,202
- 1
- 9
- 13
-
Can you explain your reasoning to multiply the probability that the first pick is less than $x$ by the probability that you land between $x$ and $x+dx$ starting at $x$? I don't understand that. Wouldn't the probability depend on what the first pick is, necessitating an integral like the one you use later on? – Feb 06 '17 at 00:32
-
1$$P(x,x) = 1/x \int_0^x P(x-z,z) dz$$ $$P(x(<1),1)=1/1\int_0^xP(x-z,z)dz$$ $$P(x(<1),1) =xP(x,x)=P(1,1)$$ – Raziman T V Feb 06 '17 at 06:16
-
8This is (proportional to) the [Dickman function](https://en.wikipedia.org/wiki/Dickman_function)! – Feb 06 '17 at 07:54
-
Just to confirm the simulation by @curious_cat, here is mine:
It's a histogram, but I drew it as a line chart because the bin sizes were quite small ($0.05$ in length, with 10 million trials of 5 iterations).
Note: vertical axis is frequency, horizontal axis is sum after 5 iterations. I found a mean of approximately $0.95$.
-
The shape of that graph does not look like I would have expected it to. It looks flat from 0 to 1 (I assume the variance seen there is entirely due to only having sampled a finite number of times). I would have expected it to start decreasing right away. And it looks like the derivative is discontinuous at 1 and nowhere else. I would have expected the derivative to be continuous. And given that the distribution can be expressed recursively I can't quite see how a single discontinuity in the derivative wouldn't cause an infinite number of discontinuities. – kasperd Feb 05 '17 at 18:44
-
That doesn't mean I think you are wrong. Just that I am surprised. I will now try to simulate it myself to see if I can reproduce your result. – kasperd Feb 05 '17 at 18:45
-
4I have proved why it has to be constant for $x<1$, please check my answer. – Raziman T V Feb 05 '17 at 19:15
-
I have done a simulation myself which produced a graph similar to yours except from an anomaly at 0 due to using discrete random numbers in the simulation. So it looks like the shape of the graph is pretty much correct. – kasperd Feb 05 '17 at 19:36
-
1For an infinite sum, the mean should be $1$ since it satisfies $\mu=\frac12 +\frac12\mu$ where $\frac12$ is the mean of a uniform random variable on $[0,1]$. For five terms in the sum it should be $\frac{2^5-1}{2^5}=\frac{31}{32}=0.96875$ – Henry Feb 09 '17 at 14:13
I just ran a quick simulation and I get a mean sum of one (standard deviation of 0.7)
Caveat: Not sure I coded it all right! Especially since I didn't test convergence.
- 219
- 1
- 7
-
4
-
3
-
3Chuck Norris could have run a quick simulation of an infinite sequence. After all, [he counted to infinity. Twice.](http://www.chucknorrisjokes.net/topjokes.php?id=604) – eipi10 Feb 08 '17 at 05:49
-
For what it's worth, I did the simulation in excel and let it cook for half a day. My histogram was essentially the same as posted above: flat from 0 to 1, then an exponential like decay. This leads to another question involving histograms, which I shall submit to the community... Recently the Israel prime minister dismissed his security staff. He was meeting Chuck Norris, and knew the Norris could personally handle any security problem. – richard1941 Feb 08 '17 at 19:12
![Comparison of simulation with numerical integral and exact formula for $x\in[1,2]$](../../images/3800239208.webp)