Is $\frac{\textrm{d}y}{\textrm{d}x}$ not a ratio?

Question

In Thomas's Calculus (11th edition), it is mentioned (Section 3.8 pg 225) that the derivative $dy/dx$ is not a ratio. Couldn't it be interpreted as a ratio, because according to the formula $dy = f'(x) \, dx$ we are able to plug in values for $dx$ and calculate a $dy$ (differential)? Then, if we rearrange we get $dy/dx=f'(x)$, and so $dy/dx$ can be seen as a ratio of $dy$ and $dx$. I wonder if the author says this because $dx$ is an independent variable, and $dy$ is a dependent variable, and for $dy/dx$ to be a ratio both variables need to be independent.

Answer 1

Historically, when Leibniz conceived of the notation, $\frac{dy}{dx}$ was supposed to be a quotient: it was the quotient of the "infinitesimal change in $y$ produced by the change in $x$" divided by the "infinitesimal change in $x$".

However, the formulation of calculus with infinitesimals in the usual setting of the real numbers leads to a lot of problems. For one thing, infinitesimals can't exist in the usual setting of real numbers! Because the real numbers satisfy an important property, called the Archimedean Property: given any positive real number $\epsilon\gt 0$, no matter how small, and given any positive real number $M\gt 0$, no matter how big, there exists a natural number $n$ such that $n\epsilon\gt M$. But an "infinitesimal" $\xi$ is supposed to be so small that no matter how many times you add it to itself, it never gets to $1$, contradicting the Archimedean Property. Other problems: Leibniz defined the tangent to the graph of $y=f(x)$ at $x=a$ by saying "Take the point $(a,f(a))$; then add an infinitesimal amount to $a$, $a+dx$, and take the point $(a+dx,f(a+dx))$, and draw the line through those two points." But if they are two different points on the graph, then it's not a tangent, and if it's just one point, then you can't define the line because you just have one point. That's just two of the problems with infinitesimals. (See below where it says "However...", though.)

So Calculus was essentially rewritten from the ground up in the following 200 years to avoid these problems, and you are seeing the results of that rewriting (that's where limits came from, for instance). Because of that rewriting, the derivative is no longer a quotient, now it's a limit: $$\lim_{h\to0 }\frac{f(x+h)-f(x)}{h}.$$ And because we cannot express this limit-of-a-quotient as a-quotient-of-the-limits (both numerator and denominator go to zero), then the derivative is not a quotient.

However, Leibniz's notation is very suggestive and very useful; even though derivatives are not really quotients, in many ways they behave as if they were quotients. So we have the Chain Rule: $$\frac{dy}{dx} = \frac{dy}{du}\;\frac{du}{dx}$$ which looks very natural if you think of the derivatives as "fractions". You have the Inverse Function theorem, which tells you that $$\frac{dx}{dy} = \frac{1}{\quad\frac{dy}{dx}\quad},$$ which is again almost "obvious" if you think of the derivatives as fractions. So, because the notation is so nice and so suggestive, we keep the notation even though the notation no longer represents an actual quotient, it now represents a single limit. In fact, Leibniz's notation is so good, so superior to the prime notation and to Newton's notation, that England fell behind all of Europe for centuries in mathematics and science because, due to the fight between Newton's and Leibniz's camp over who had invented Calculus and who stole it from whom (consensus is that they each discovered it independently), England's scientific establishment decided to ignore what was being done in Europe with Leibniz notation and stuck to Newton's... and got stuck in the mud in large part because of it.

(Differentials are part of this same issue: originally, $dy$ and $dx$ really did mean the same thing as those symbols do in $\frac{dy}{dx}$, but that leads to all sorts of logical problems, so they no longer mean the same thing, even though they behave as if they did.)

So, even though we write $\frac{dy}{dx}$ as if it were a fraction, and many computations look like we are working with it like a fraction, it isn't really a fraction (it just plays one on television).

However... There is a way of getting around the logical difficulties with infinitesimals; this is called nonstandard analysis. It's pretty difficult to explain how one sets it up, but you can think of it as creating two classes of real numbers: the ones you are familiar with, that satisfy things like the Archimedean Property, the Supremum Property, and so on, and then you add another, separate class of real numbers that includes infinitesimals and a bunch of other things. If you do that, then you can, if you are careful, define derivatives exactly like Leibniz, in terms of infinitesimals and actual quotients; if you do that, then all the rules of Calculus that make use of $\frac{dy}{dx}$ as if it were a fraction are justified because, in that setting, it is a fraction. Still, one has to be careful because you have to keep infinitesimals and regular real numbers separate and not let them get confused, or you can run into some serious problems.

Answer 2

Just to add some variety to the list of answers, I'm going to go against the grain here and say that you can, in an albeit silly way, interpret $dy/dx$ as a ratio of real numbers.

For every (differentiable) function $f$, we can define a function $df(x; dx)$ of two real variables $x$ and $dx$ via $$df(x; dx) = f'(x)\,dx.$$ Here, $dx$ is just a real number, and no more. (In particular, it is not a differential 1-form, nor an infinitesimal.) So, when $dx \neq 0$, we can write: $$\frac{df(x;dx)}{dx} = f'(x).$$

---

All of this, however, should come with a few remarks.

It is clear that these notations above do not constitute a definition of the derivative of $f$. Indeed, we needed to know what the derivative $f'$ meant before defining the function $df$. So in some sense, it's just a clever choice of notation.

But if it's just a trick of notation, why do I mention it at all? The reason is that in higher dimensions, the function $df(x;dx)$ actually becomes the focus of study, in part because it contains information about all the partial derivatives.

To be more concrete, for multivariable functions $f\colon R^n \to R$, we can define a function $df(x;dx)$ of two n-dimensional variables $x, dx \in R^n$ via $$df(x;dx) = df(x_1,\ldots,x_n; dx_1, \ldots, dx_n) = \frac{\partial f}{\partial x_1}dx_1 + \ldots + \frac{\partial f}{\partial x_n}dx_n.$$

Notice that this map $df$ is linear in the variable $dx$. That is, we can write: $$df(x;dx) = (\frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n}) \begin{pmatrix} dx_1 \\ \vdots \\ dx_n \\ \end{pmatrix} = A(dx),$$ where $A$ is the $1\times n$ row matrix of partial derivatives.

In other words, the function $df(x;dx)$ can be thought of as a linear function of $dx$, whose matrix has variable coefficients (depending on $x$).

So for the $1$-dimensional case, what is really going on is a trick of dimension. That is, we have the variable $1\times1$ matrix ($f'(x)$) acting on the vector $dx \in R^1$ -- and it just so happens that vectors in $R^1$ can be identified with scalars, and so can be divided.

Finally, I should mention that, as long as we are thinking of $dx$ as a real number, mathematicians multiply and divide by $dx$ all the time -- it's just that they'll usually use another notation. The letter "$h$" is often used in this context, so we usually write $$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h},$$ rather than, say, $$f'(x) = \lim_{dx \to 0} \frac{f(x+dx) - f(x)}{dx}.$$ My guess is that the main aversion to writing $dx$ is that it conflicts with our notation for differential $1$-forms.

EDIT: Just to be even more technical, and at the risk of being confusing to some, we really shouldn't even be regarding $dx$ as an element of $R^n$, but rather as an element of the tangent space $T_xR^n$. Again, it just so happens that we have a canonical identification between $T_xR^n$ and $R^n$ which makes all of the above okay, but I like distinction between tangent space and euclidean space because it highlights the different roles played by $x \in R^n$ and $dx \in T_xR^n$.

Answer 3

My favorite "counterexample" to the derivative acting like a ratio: the implicit differentiation formula for two variables. We have $$\frac{dy}{dx} = -\frac{\partial F/\partial x}{\partial F/\partial y} $$

The formula is almost what you would expect, except for that pesky minus sign.

See Implicit differentiation for the rigorous definition of this formula.

Answer 4

It is best to think of $\frac{d}{dx}$ as an operator which takes the derivative, with respect to $x$, of whatever expression follows.

Answer 5

In Leibniz's mathematics, if $y=x^2$ then $\frac{dy}{dx}$ would be "equal" to $2x$, but the meaning of "equality" to Leibniz was not the same as it is to us. He emphasized repeatedly (for example in his 1695 response to Nieuwentijt) that he was working with a generalized notion of equality "up to" a negligible term. Also, Leibniz used several different pieces of notation for "equality". One of them was the symbol "$\,{}_{\ulcorner\!\urcorner}\,$". To emphasize the point, one could write $$y=x^2\quad \rightarrow \quad \frac{dy}{dx}\,{}_{\ulcorner\!\urcorner}\,2x$$ where $\frac{dy}{dx}$ is literally a ratio. When one expresses Leibniz's insight in this fashion, one is less tempted to commit an ahistorical error of accusing him of having committed a logical inaccuracy.

In more detail, $\frac{dy}{dx}$ is a true ratio in the following sense. We choose an infinitesimal $\Delta x$, and consider the corresponding $y$-increment $\Delta y = f(x+\Delta x)-f(x)$. The ratio $\frac{\Delta y}{\Delta x}$ is then infinitely close to the derivative $f'(x)$. We then set $dx=\Delta x$ and $dy=f'(x)dx$ so that $f'(x)=\frac{dy}{dx}$ by definition. One of the advantages of this approach is that one obtains an elegant proof of chain rule $\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$ by applying the standard part function to the equality $\frac{\Delta y}{\Delta x}=\frac{\Delta y}{\Delta u}\frac{\Delta u}{\Delta x}$.

In the real-based approach to the calculus, there are no infinitesimals and therefore it is impossible to interpret $\frac{dy}{dx}$ as a true ratio. Therefore claims to that effect have to be relativized modulo anti-infinitesimal foundational commitments.

Note 1. I recently noticed that Leibniz's $\,{}_{\ulcorner\!\urcorner}\,$ notation occurs several times in Margaret Baron's book The origins of infinitesimal calculus, starting on page 282. It's well worth a look.

Note 2. It should be clear that Leibniz did view $\frac{dy}{dx}$ as a ratio. (Some of the other answers seem to be worded ambiguously with regard to this point.)

Answer 6

Typically, the $\frac{dy}{dx}$ notation is used to denote the derivative, which is defined as the limit we all know and love (see Arturo Magidin's answer). However, when working with differentials, one can interpret $\frac{dy}{dx}$ as a genuine ratio of two fixed quantities.

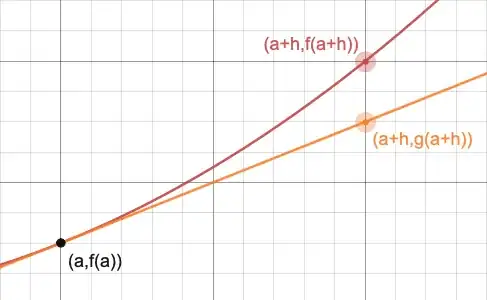
Draw a graph of some smooth function $f$ and its tangent line at $x=a$. Starting from the point $(a, f(a))$, move $dx$ units right along the tangent line (not along the graph of $f$). Let $dy$ be the corresponding change in $y$.

So, we moved $dx$ units right, $dy$ units up, and stayed on the tangent line. Therefore the slope of the tangent line is exactly $\frac{dy}{dx}$. However, the slope of the tangent at $x=a$ is also given by $f'(a)$, hence the equation

$$\frac{dy}{dx} = f'(a)$$

holds when $dy$ and $dx$ are interpreted as fixed, finite changes in the two variables $x$ and $y$. In this context, we are not taking a limit on the left hand side of this equation, and $\frac{dy}{dx}$ is a genuine ratio of two fixed quantities. This is why we can then write $dy = f'(a) dx$.

Answer 7

Of course it is a ratio.

$dy$ and $dx$ are differentials. Thus they act on tangent vectors, not on points. That is, they are functions on the tangent manifold that are linear on each fiber. On the tangent manifold the ratio of the two differentials $\frac{dy}{dx}$ is just a ratio of two functions and is constant on every fiber (except being ill defined on the zero section) Therefore it descends to a well defined function on the base manifold. We refer to that function as the derivative.

As pointed out in the original question many calculus one books these days even try to define differentials loosely and at least informally point out that for differentials $dy = f'(x) dx$ (Note that both sides of this equation act on vectors, not on points). Both $dy$ and $dx$ are perfectly well defined functions on vectors and their ratio is therefore a perfectly meaningful function on vectors. Since it is constant on fibers (minus the zero section), then that well defined ratio descends to a function on the original space.

At worst one could object that the ratio $\frac{dy}{dx}$ is not defined on the zero section.

Answer 8

The notation $dy/dx$ - in elementary calculus - is simply that: notation to denote the derivative of, in this case, $y$ w.r.t. $x$. (In this case $f'(x)$ is another notation to express essentially the same thing, i.e. $df(x)/dx$ where $f(x)$ signifies the function $f$ w.r.t. the dependent variable $x$. According to what you've written above, $f(x)$ is the function which takes values in the target space $y$).

Furthermore, by definition, $dy/dx$ at a specific point $x_0$ within the domain $x$ is the real number $L$, if it exists. Otherwise, if no such number exists, then the function $f(x)$ does not have a derivative at the point in question, (i.e. in our case $x_0$).

For further information you can read the Wikipedia article: http://en.wikipedia.org/wiki/Derivative

Answer 9

$\boldsymbol{\dfrac{dy}{dx}}$ is definitely not a ratio - it is the limit (if it exists) of a ratio. This is Leibniz's notation of the derivative (c. 1670) which prevailed to the one of Newton $\dot{y}(x)$.

Still, most Engineers and even many Applied Mathematicians treat it as a ratio. A very common such case is when solving separable ODEs, i.e. equations of the form $$ \frac{dy}{dx}=f(x)g(y), $$ writing the above as $$f(x)\,dx=\frac{dy}{g(y)}, $$ and then integrating.

Apparently this is not Mathematics, it is a symbolic calculus.

Why are we allowed to integrate the left hand side with respect to to $x$ and the right hand side with respect to to $y$? What is the meaning of that?

This procedure often leads to the right solution, but not always. For example applying this method to the IVP $$ \frac{dy}{dx}=y+1, \quad y(0)=-1,\qquad (\star) $$ we get, for some constant $c$, $$ \ln (y+1)=\int\frac{dy}{y+1} = \int dx = x+c, $$ equivalently $$ y(x)=\mathrm{e}^{x+c}-1. $$ Note that it is impossible to incorporate the initial condition $y(0)=-1$, as $\mathrm{e}^{x+c}$ never vanishes. By the way, the solution of $(\star)$ is $y(x)\equiv -1$.

Even worse, consider the case of the IVP $$ y'=\frac{3y^{1/3}}{2}, \quad y(0)=0. \tag{$\star\star$} $$ This IVP does not enjoy uniqueness. It possesses infinitely many solutions. Nevertheless, using this symbolic calculus, we obtain that $y^{2/3}=x$, which is one of the infinitely many solutions of $(\star\star)$. Another one is $y\equiv 0$.

In my opinion, Calculus should be taught rigorously, with $\delta$'s and $\varepsilon$'s. Once these are well understood, then one can use such symbolic calculus, provided that he/she is convinced under which restrictions it is indeed permitted.

Answer 10

It is not a ratio, just as $dx$ is not a product.

Answer 11

In most formulations, $\frac{dx}{dy}$ can not be interpreted as a ratio, as $dx$ and $dy$ do not actually exist in them. An exception to this is shown in this book. How it works, as Arturo said, is we allow infinitesimals (by using the hyperreal number system). It is well formulated, and I prefer it to limit notions, as this is how it was invented. Its just that they weren't able to formulate it correctly back then. I will give a slightly simplified example. Let us say you are differentiating $y=x^2$. Now let $dx$ be a miscellaneous infinitesimals (it is the same no matter which you choose if your function is differentiate-able at that point.) $$dy=(x+dx)^2-x^2$$ $$dy=2x\times dx+dx^2$$ Now when we take the ratio, it is: $$\frac{dy}{dx}=2x+dx$$

(Note: Actually,$\frac{\Delta y}{\Delta x}$ is what we found in the beginning, and $dy$ is defined so that $\frac{dy}{dx}$ is $\frac{\Delta y}{\Delta x}$ rounded to the nearest real number.)

Answer 12

$\frac{dy}{dx}$ is not a ratio - it is a symbol used to represent a limit.

Answer 13

I realize this is an old post, but I think it's worth while to point out that in the so-called Quantum Calculus $\frac{dy}{dx}$ $is$ a ratio. The subject $starts$ off immediately by saying this is a ratio, by defining differentials and then calling derivatives a ratio of differentials:

The $q-$differential is defined as

$$d_q f(x) = f(qx) - f(x)$$

and the $h-$differential as $$d_h f(x) = f(x+h) - f(x)$$

It follows that $d_q x = (q-1)x$ and $d_h x = h$.

From here, we go on to define the $q-$derivative and $h-$derivative, respectively:

$$D_q f(x) = \frac{d_q f(x)}{d_q x} = \frac{f(qx) - f(x)}{(q-1)x}$$

$$D_h f(x) = \frac{d_h f(x)}{d_q x} = \frac{f(x+h) - f(x)}{h}$$

Notice that

$$\lim_{q \to 1} D_q f(x) = \lim_{h\to 0} D_h f(x) = \frac{df(x)}{x} \neq \text{a ratio}$$

Answer 14

To ask "Is $\frac{dy}{dx}$ a ratio or isn't it?" is like asking "Is $\sqrt 2$ a number or isn't it?" The answer depends on what you mean by "number". $\sqrt 2$ is not an Integer or a Rational number, so if that's what you mean by "number", then the answer is "No, $\sqrt 2$ is not a number."

However, the Real numbers are an extension of the Rational numbers that includes irrational numbers such as $\sqrt 2$, and so, in this set of numbers, $\sqrt 2$ is a number.

In the same way, a differential such as $dx$ is not a Real number, but it is possible to extend the Real numbers to include infinitesimals, and, if you do that, then $\frac{dy}{dx}$ is truly a ratio.

When a professor tells you that $dx$ by itself is meaningless, or that $\frac{dy}{dx}$ is not a ratio, they are correct, in terms of "normal" number systems such as the Real or Complex systems, which are the number systems typically used in science, engineering and even mathematics. Infinitesimals can be placed on a rigorous footing, but sometimes at the cost of surrendering some important properties of the numbers we rely on for everyday science.

See https://en.wikipedia.org/wiki/Infinitesimal#Number_systems_that_include_infinitesimals for a discussion of number systems that include infinitesimals.

Answer 15

Assuming you're happy with $dy/dx$, when it becomes $\ldots dy$ and $\ldots dx$ it means that it follows that what precedes $dy$ in terms of $y$ is equal to what precedes $dx$ in terms of $x$.

"in terms of" = "with reference to".

That is, if "$a \frac{dy}{dx} = b$", then it follows that "$a$ with reference to $y$ = $b$ with reference to $x$". If the equation has all the terms with $y$ on the left and all with $x$ on the right, then you've got to a good place to continue.

The phrase "it follows that" means you haven't really moved $dx$ as in algebra. It now has a different meaning which is also true.

Answer 16

Anything that can be said in mathematics can be said in at least 3 different ways...all things about derivation/derivatives depend on the meaning that is attached to the word: TANGENT. It is agreed that the derivative is the "gradient function" for tangents (at a point); and spatially (geometrically) the gradient of a tangent is the "ratio" ( "fraction" would be better ) of the y-distance to the x-distance. Similar obscurities occur when "spatial and algebraic" are notationally confused.. some people take the word "vector" to mean a track!

Answer 17

There are many answers here, but the simplest seems to be missing. So here it is:

Yes, it is a ratio, for exactly the reason that you said in your question.

Answer 18

I am going to join @Jesse Madnick here, and try to interpret $\frac{dy}{dx}$ as a ratio. The idea is: lets interpret $dx$ and $dy$ as functions on $T\mathbb R^2$, as if they were differential forms. For each tangent vector $v$, set $dx(v):=v(x)$. If we identify $T\mathbb R^2$ with $\mathbb R^4$, we get that $(x,y,dx,dy)$ is just the canonical coordinate system for $\mathbb R^4$. If we exclude the points where $dx=0$, then $\frac{dy}{dx} = 2x$ is a perfectly healthy equation, its solutions form a subset of $\mathbb R^4$.

Let's see if it makes any sense. If we fix $x$ and $y$, the solutions form a straight line through the origin of the tangent space at $(x,y)$, its slope is $2x$. So, the set of all solutions is a distribution, and the integral manifolds happen to be the parabolas $y=x^2+c$. Exactly the solutions of the differential equation that we would write as $\frac{dy}{dx} = 2x$. Of course, we can write it as $dy = 2xdx$ as well. I think this is at least a little bit interesting. Any thoughts?

Answer 19

The derivate $\frac{dy}{dx}$ is not a ratio, but rather a representation of a ratio within a limit.

Similarly, $dx$ is a representation of $\Delta x$ inside a limit with interaction. This interaction can be in the form of multiplication, division, etc. with other things inside the same limit.

This interaction inside the limit is what makes the difference. You see, a limit of a ratio is not necessarily the ratio of the limits, and that is one example of why the interaction is considered to be inside the limit. This limit is hidden or left out in the shorthand notation that Liebniz invented.

The simple fact is that most of calculus is a shorthand representation of something else. This shorthand notation allows us to calculate things more quickly and it looks better than what it is actually representative of. The problem comes in when people expect this notation to act like actual maths, which it can't because it is just a representation of actual maths.

So, in order to see the underlying properties of calculus, we always have to convert it to the actual mathematical form and then analyze it from there. Then by memorization of basic properties and combinations of these different properties we can derive even more properties.

Answer 20

$dy/dx$ is quite possibly the most versatile piece of notation in mathematics. It can be interpreted as

1. A shorthand for the limit of a quotient: $$ \frac{dy}{dx}=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x} \, .$$
2. The result of applying the derivative operator, $d/dx$, on a given expression $y$.
3. The ratio of two infinitesimals $dy$ and $dx$ (with this interpretation made rigorous using non-standard analysis).
4. The ratio of two differentials $dy$ and $dx$ acting along the tangent line to a given curve.

All of these interpretations are equally valid and useful in their own way. In interpretations (1) and (2), which are the most common, $dy/dx$ is not seen as a ratio, despite the fact that it often behaves as one. Interpretations (3) and (4) offer viable alternatives. Since Mikhail Katz has already given a good exposition of infinitesimals, let me focus the remainder of this answer on interpretation (4).

Given a curve $y=f(x)$, the equation of the line tangent to the point $(a,f(a))$ is given by $$ g(x)=f'(a)(x-a)+f(a) \, . $$ This tangent line provides us with a linear approximation of a function around a given point. For small $h$, the value of $f(a+h)$ is roughly equal to $g(a+h)$. Hence, $$ f(a+h) \approx f(a) + f'(a)h $$ The linear approximation formula has a very clear geometric meaning, where you imagine staying on the tangent line rather than the curve itself:

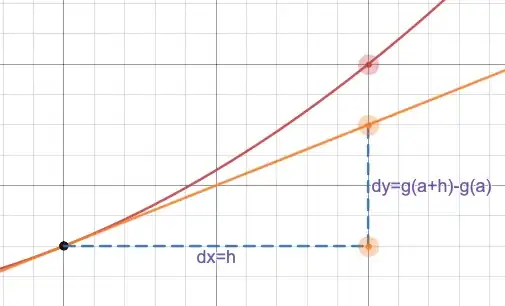
We can then define $dx=h$ and $dy=g(a+h)-g(a)$:

Since the tangent line has a constant gradient, we have $$ \frac{dy}{dx}=\frac{g(a+h)-g(a)}{h}=g'(a)=f'(a) \, , $$ provided that $dx$ is non-zero. Here, $dy$ and $dx$ are genuine quantities that act along the tangent line to the curve, and can be manipulated like numbers becasuse they are numbers.

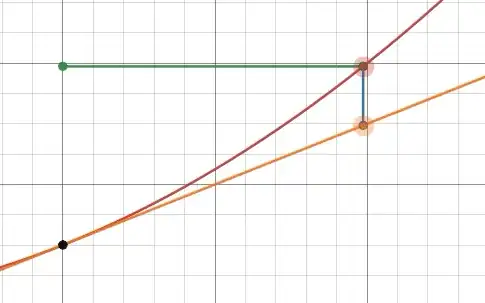
This notion of $dy/dx$ becomes very useful when you realise that, in a very meaningful sense, the tangent line is the best linear approximation of a function around a given point. We can turn the linear approximation formula into an exact equality by letting $r(h)$ be the remainder term: $$ f(a+h)=g(a+h)+r(h)=f(a)+f'(a)h+r(h) \, . $$ As $h\to0$, $r(h)\to0$. In fact, the remainder term satisifes a stronger condition: $$ \lim_{h \to 0}\frac{r(h)}{h}=0 \, . $$ The fact that the above limit is equal to $0$ demonstrates just how good the tangent line is at approximating the local behaviour of a function. It's not that impressive that when $h$ is small, $r(h)$ is also very small (any good approximation should have this property). What makes the tangent line unique is that when $h$ is small, $r(h)$ is orders of magnitude smaller, meaning that the 'relative error' is tiny. This relative error is showcased in the below animation, where the length of the green line is $h$, whereas the length of the blue line is $r(h)$:

Seen in this light, the statement $$ \frac{dy}{dx}=f'(a) $$ is an expression of equality between the quotient of two numbers $dy$ and $dx$, and the derivative $f'(a)$. It makes perfect sense to multiply both sides by $dx$, to get $$ dy=f'(a)dx \, , $$ Note that $dy+r(h)=f(a+h)-f(a)$, and so \begin{align} f(a+h)-f(a) - r(h) &= f'(a)h \\ f(a+h) &= f(a) + f'(a)h + r(h) \, , \end{align} which gives us another notion of the derivative, through the lense of linear approximation.

Answer 21

The best way to understand $d$ is that of being an operator, with a simple rule

$$df(x)=f'(x)dx$$

If you take this definition then $dy/dx$ is indeed a ratio as it is stripping $f'(x)dx$ of $dx$

$$\frac{dy}{dx}=\frac{y'dx}{dx}=y'$$

This is done in the same manner as $12/3$ is stripping $12=4\cdot3$ of $3$

Answer 22

In a certain context, $\frac{dy}{dx}$ is a ratio.

$\frac{dy}{dx}=s$ means:

Standard calculus

$\forall \epsilon\ \exists \delta\ \forall dx$

If $0<|dx|\leq\delta$

If $(x, y) = (x_0, y_0)$, but $(x, y)$ also could have been $(x_0+dx, y_0+\Delta y)$

If $dy = sdx$

Then $\left|\frac{\Delta y}{dx}-\frac{dy}{dx}\right|\leq \epsilon$

Nonstandard calculus

$\forall dx$ where $dx$ is a nonzero infinitessimal

$\exists \epsilon$ where $\epsilon$ is infinitessimal

If $(x, y) = (x_0, y_0)$, but $(x, y)$ also could have been $(x_0+dx, y_0+\Delta y)$

If $dy = sdx$

Then $\frac{\Delta y}{dx} - \frac{dy}{dx} = \epsilon$

---

In either case, $dx$ gets its meaning from the restriction placed on it (which is described using quantifiers), and $dy$ gets its meaning from the value of $s$ and the restriction placed on $dx$.

Therefore, it makes sense to make a statement about $\frac{dy}{dx}$ as a ratio if the statement is appropriately quantified and $dx$ is appropriately restricted.

Less formally, $dx$ is understood as "the amount by which $x$ is nudged", $dx$ is understood as "the amount by which $y$ is nudged on the tangent line", and $\Delta y$ is understood as "the amount by which $y$ is nudged on the curve". This is a perfectly sensible way to talk about a rough intuition.

Answer 23

Of course it is a fraction in appropriate definition.

Let me add my view of answer, which is updated text from some other question.

Accordingly, for example, Murray H. Protter, Charles B. Jr. Morrey - Intermediate Calculus-(2012) page 231 differential for function $f:\mathbb{R} \to \mathbb{R}$ is defined as function of two variables selected in special way by formula: $$df(x)(h)=f'(x)h$$ so it is linear function with respect to $h$ approximating $f$ in point $x$. Also it can be called 1-form.

This is fully rigorous definition, which does not required anything, then definition/existence of derivative. But here is more: if we define differential as existence of linear approximation in point $x=x_0$ for which holds $$f(x)-f(x_0) = A(x-x_0) + o(x-x_0), x \to x_0$$ then from this we obtain, that $f$ have derivative in point $x=x_0$ and $A=f'(x_0)$. So existence of derivative and existence of differential are equivalence requirements. Rudin W. - Principles of mathematical analysis-(1976) page 213.

If we use this definition for identity function $g(x)=x$, then we obtain $$dg(x)(h)=dx(h)=g'(x)h=h$$ This gives possibility to understand record $\frac{dy}{dx}=\frac{df}{dx}$ exactly as usual fraction of differentials and holds equality $\frac{df(x)}{dx}=f'(x)$. Exact record is $\frac{df(x)(h)}{dx(h)}=\frac{f'(x)h}{h}=f'(x)$.

Let me note, that we are speaking about single variable approach, not multivariable.

I cannot explain why someone assert, that $\frac{dy}{dx}$ cannot be understand as fraction - may be lack of knowledge about differential definition? For any case I bring, additionally to above source, list of books where is definition of differential which gives possibility understand fraction in question:

1. James R. Munkres - Analysis on manifolds-(1997) 252-253 p.
2. Vladimir A. Zorich - Mathematical Analysis I- (2016) 176 p.
3. Loring W. Tu (auth.) - An introduction to manifolds-(2011) 34 p.
4. Herbert Amann, Joachim Escher - Analysis II (v. 2) -(2008) 38 p.
5. Robert Creighton Buck, Ellen F. Buck - Advanced Calculus-(1978) 343 p.
6. Rudin W. - Principles of mathematical analysis-(1976) 213 p.
7. Fichtenholz Gr. M - Course of Differential and Integral Calculus vol. 1 2003 240-241 p.
8. Richard Courant - Differential and Integral Calculus, Vol. I, 2nd Edition -Interscience Publishers (1937), page 107
9. John M.H. Olmsted - Advanced calculus-Prentice Hall (1961), page 90.
10. David Guichard - Single and Multivariable Calculus_ Early Transcendentals (2017), page 144
11. Stewart, James - Calculus-Cengage Learning (2016), page 190
12. Differential in Calculus

For complete justice I mention Michael Spivak - Calculus (2008) 155 p. where author is against understanding of fractions, but argument is from kind "it is not, because it cannot be". Spivak one of my most respected and favorite authors, but "Amicus Plato, sed magis amica veritas".

Answer 24

While it can be approximated by a ratio, the derivative itself is actuality the limit of a ratio. This is made more apparent when one moves to partial derivatives and $\frac{1}{\partial y/ \partial x}\neq\partial x / \partial y$ The concept of $dx$ being an actual number and the derivative being an actual ratio is mainly a heuristic device that can get useful intuitions if used properly.

Answer 25

If I give my answer from an eye of physicist ,then you may think of following-

For a particle moving along $x$-axis with variable velocity, We define instantaneous velocity $v$ of an object as rate of change of x-coordinate of particle at that instant and since we define "rate of change", therefore it must be equal to total change divided by time taken to bring that change. since we have to calculate the instantaneous velocity. we assume instant to mean " an infinitesimally short interval of time for which particle can be assumed to be moving with constant velocity and denote this infinitesimal time interval by $dt$. Now particle cannot go more than an infinitesimal distance $dx$ in an infinitesimally small time. therefore we define instantaneous velocity as

$v=\frac{dx}{dt}$ i.e. as ratio of two infinitesimal changes.

This also helps us to get correct units for velocity since for change in position it will be $m$ and for change in time it will be $s$.

While defining pressure at a point, acceleration, momentum, electric current through a cross section etc. we assume ratio of two infinitesimal quantities.

So I think for practical purposes you may assume it to be a ratio but what actually it is has been well clarified in other answers.

Also from my knowledge of mathematics, when I learnt about differentiating a function also provides slope of tangent, I was told that Leibniz assumed the smooth curve of some function to be made of infinite number infinitesimally small lines joined together ,extending any one of them gives tangent to curve and the slope of that infinitesimally small line = $\frac{dy}{dx}$ = slope of tangent that we get on extending that line.

Even I learnt that we would need a magnifying glass of "infinite zoom in power" to see those lines which may not be possible in real.

Answer 26

It is incorrect to call it a ratio but it's very handy to visualize it as a ratio where the $\frac{l}{\delta} $ talks about the times a certain $l>0$ can be divided by saying an exceedingly small $\delta>0$ such that there is an exceedingly small remainder. Now if even $l$ is exceedingly small then the relative difference of the two changes can be measured using this "ratio". The idea of limits suggests that these two values $l$ and $\delta$, are themselves changing or $l$ changes with $\delta$ and the sole reason this can't be a ratio is that ratios are defined for constant fractions whilst $\frac{d}{dx} $ is a changing fraction with no concept of a remainder.