Deriving the inverse of a 2x2 matrix

Question

I am looking for a derivation for the inverse of a 2x2 matrix. I am also wondering why the determinant is involved in the expression. I am familiar with high school maths and linear algebra. If there is an intuitive reason for expression i would also be interested in that.

Answer 1

How to derive the inverse matrix:

Start with the augmented matrix $$\left(\begin{array}{cc|cc} a & c & 1 & 0 \\ b & d & 0 & 1\end{array}\right)$$

and perform Gaussian elimination until you get $$\left(\begin{array}{cc|cc} 1 & 0 & ? & ? \\ 0 & 1 & ? & ?\end{array}\right)$$

Then the matrix $\pmatrix{? & ? \\ ? & ?}$ will be the inverse of $\pmatrix{a & c \\ b & d}$. Try it yourself.

For Further Reference:

• Method for Finding Matrix-Inverse Through Gauss-Jordan?
• Why does the Gaussian-Jordan elimination works when finding the inverse matrix?
• Inverting $2\times 2$ matrices

Intuition on why a factor of $\frac{1}{\det(A)}$ shows up:

Intuitively, a matrix is just a representation of some linear transformation. In particular, when you see the matrix $\pmatrix{a & c \\ b & d}$, you should think of this as the function $f(x,y) = (ax+cy,bx+dy)$.

For Further Reference:

• Correspondences between linear transformations and matrices
• Understanding matrices as linear transformations & Relationship with Gaussian Elimination and Bézout's Identity
• Matrix multiplication: interpreting and understanding the process
• difference between linear transformation and its matrix representation .

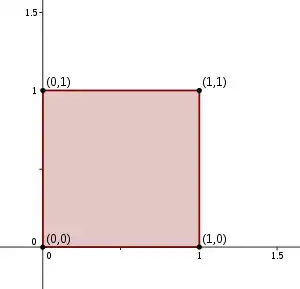
The determinant of a matrix is the scale factor by which the transformation changes the $n$-volume of the unit $n$-cube. In the $2\times 2$ case notice that $f$ (i.e. the matrix $\pmatrix{a & c \\ b & d}$) maps the $4$ vertices of the unit square -- $(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$ -- to the new points $(0,0)$, $(a,b)$, $(a+c,b+d)$, $(c,d)$. You can confirm for yourself that the area of the quadrilateral with these new vertices is $ad-bc$.

For Further Reference:

• What's an intuitive way to think about the determinant?

So why does the reciprocal of the determinant show up in the inverse matrix? Well remember what the inverse matrix is -- it's the matrix $A^{-1}$ such that $AA^{-1} = I = A^{-1}A$. So when you multiply the matrix by its inverse you should get the identity matrix. Or using our intuition about matrices just being a way to represent linear transformations, we can say that the inverse matrix represents the function $f^{-1}$ which when composed with our original function $f$ gives the identity function. So then, if $f$ scales the unit square by $ad-bc$, then the inverse function must scale by $\frac{1}{ad-bc}$ so that when they're composed they cancel out.

Answer 2

The easiest way to see why the determinant is involved is to just do the calculation, $$ \pmatrix{a&b\cr c&d\cr}\pmatrix{d&-b\cr-c&a\cr}=\pmatrix{ad-bc&0\cr0&ad-bc\cr}=(\det A)I $$ from which it is immediate that $$ \pmatrix{a&b\cr c&d\cr}^{-1}={1\over\det A}\pmatrix{d&-b\cr-c&a\cr} $$ (provided $\det A\ne0$).

Answer 3

If $B=\left( \begin{array}{cc} l & r \\ n & m \end{array} \right)$ is the inverse of $A$ and $A = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right),$ then you know that $$AB=\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right),$$ and so you end up with the following system of equations: $$al+bn=1\\ar+bm=0\\cl+dn=0\\cr+dm=1,$$ So if you multiply, say the first equation by $d$ and third equation by $b$ and you subtract them, you get something like $d(al+bn)-b(cl+dn)=d$ and so $$dal+dbn-bcl-bdn=d\\dal-bcl=d\\l(da-bc)=d\\l=\frac{d}{da-bc}.$$ that if you know that $da-bc=det(A)\neq 0.$ You will end up with that if you do it for all the variables involved.
Hope it helps.