124

Two events are mutually exclusive if they can't both happen.

Independent events are events where knowledge of the probability of one doesn't change the probability of the other.

Are these definitions correct? If possible, please give more than one example and counterexample.

NNOX Apps
  • 1
  • 15
  • 118
  • 216
Adnan Ali
  • 1,413
  • 4
  • 11
  • 10
  • 14
    They are, in a sense, completely opposite features. If $A$ and $B$ are independent, knowledge that $A$ occurred does not change the probabilities that $B$ may have occurred. Where as if $A$ and $B$ are disjoint, knowledge that $A$ occurred completely changes the probabilities that $B$ may have occurred by collapsing them to $0$. – 2'5 9'2 Feb 02 '16 at 22:56
  • I just noticed that the definitions in this question look like they've been taken from my answer [here](http://math.stackexchange.com/questions/13367/doubts-on-mutually-exclusive-and-independent-events?rq=1). (Not that I mind or anything.) – Oscar Cunningham Feb 19 '16 at 09:50
  • Consider taking out a card from a deck of $52$ playing cards. $S$: The card is a spade. $A$: The card is an ace. The two events are not mutually exclusive as there exists an Ace of Spades. $P(A) = \frac{4}{52}$ and $P(S) = \frac{1}{4}$. and $P(A\cap S) = \frac{1}{52} = \frac{4}{52} \frac{1}{4} = P(A) P(S)$ – dark32 Mar 19 '17 at 13:21
  • @alex.jordan If you wanted to highlight the analogy, you could say that independence and mutual exclusivity were defined by $P(AB)=P(A)P(B)$ and $P(A+B)=P(A)+P(B)$ respectively. – Oscar Cunningham Apr 11 '17 at 18:21
  • The book Counterexamples in Probability (Third Edition) by J. M. Stoyanov (Dover, 2013) is a treasure trove of information. In particular, Section 3 of Chapter 1 explores INDEPENDENCE OF RANDOM EVENTS. – PolyaPal Nov 28 '17 at 18:07
  • Does this answer your question? [Independent and mutually exclusive](https://math.stackexchange.com/questions/332378/independent-and-mutually-exclusive) – NNOX Apps Dec 24 '21 at 08:58

8 Answers8

125

Yes, that's fine.

Events are mutually exclusive if the occurrence of one event excludes the occurrence of the other(s). Mutually exclusive events cannot happen at the same time. For example: when tossing a coin, the result can either be heads or tails but cannot be both.

$$\left.\begin{align}P(A\cap B) &= 0 \\ P(A\cup B) &= P(A)+P(B)\\ P(A\mid B)&=0 \\ P(A\mid \neg B) &= \frac{P(A)}{1-P(B)}\end{align}\right\}\text{ mutually exclusive }A,B$$

Events are independent if the occurrence of one event does not influence (and is not influenced by) the occurrence of the other(s). For example: when tossing two coins, the result of one flip does not affect the result of the other.

$$\left.\begin{align}P(A\cap B) &= P(A)P(B) \\ P(A\cup B) &= P(A)+P(B)-P(A)P(B)\\ P(A\mid B)&=P(A) \\ P(A\mid \neg B) &= P(A)\end{align}\right\}\text{ independent }A,B$$

This of course means mutually exclusive events are not independent, and independent events cannot be mutually exclusive. (Events of measure zero excepted.)

Graham Kemp
  • 119,730
  • 6
  • 49
  • 108
  • can i get a real life example for better understanding. take a look i have edited Question and made it more clear. – Adnan Ali Sep 22 '14 at 05:48
  • 10
    "This of course means..." Events of probability zero excluded. – Did Sep 22 '14 at 06:21
  • 1
    Is there any connection between independent events and mutually exclusive events? I meant to ask "If $A$ and $B$ are mutually exclusive, what can be commented on the independence of $A$ and $B$ or vice versa." Or is there no such connection at all? I guess there is none. But just want to confirm. – Maha May 23 '15 at 15:22
  • 4
    @Mahesha999 If two events are mutually exclusive, then they are NOT independent. – Pramod Jun 24 '15 at 01:11
  • I think the hint is, in Independent events, there are usually two or more events involved considered as a whole. – Anwar Feb 09 '17 at 05:10
  • 1
    @Anwar "Yes, that's fine" is the wrong answer to your question because it is not correct to say the "knowledge of the probability" changes the probability that an event happens. The "knowledge of the probability" never changes anything. The occurence of an event changes the probability as Graham explains in his answer. – miracle173 Mar 12 '17 at 07:59
  • @Did Loved your one liner! The wording "mutual", "exclusiveness" is rather elusive. One could almost and nearly come to think conventionally, exclusive as independent. Learning, knowledge, concepts pretty much boils down to jargon of the context. Phew! – bonCodigo Mar 28 '17 at 20:22
  • How do you know the last property of mutually exclusive events? what is the intuition behind it? – user485656 Oct 24 '17 at 23:39
  • @user485656 Which last property? – Graham Kemp Oct 25 '17 at 00:30
  • @GrahamKemp probability of A given Not(B) – user485656 Oct 26 '17 at 21:41
  • 1
    If $A$ is independent from $B$, then it is independent from $\neg B$. – Graham Kemp Oct 27 '17 at 02:50
  • @Pramod, is there a proof of that statement? – HeWhoMustBeNamed Dec 04 '17 at 15:42
  • @HeWhoMustBeNamed That's exactly what the above answer shows. If the events A and B are mutually exclusive, then the occurrence of A renders the probability of B to occur $= 0$. This is because A and B can't occur at the same time. However, there is an exception to this. If $P(B) = 0$, then regardless of if A occurred or not, $P(B)$ remains $0$. – Ardent Apr 09 '21 at 07:57
24

After reading the answers above I still could not understand clearly the difference between mutually exclusive AND independent events. I found a nice answer from Dr. Pete posted on math forum. So I attach it here so that op and many other confused guys like me could save some of their time.

If two events A and B are independent a real-life example is the following. Consider a fair coin and a fair six-sided die. Let event A be obtaining heads, and event B be rolling a 6. Then we can reasonably assume that events A and B are independent, because the outcome of one does not affect the outcome of the other. The probability that both A and B occur is

P(A and B) = P(A)P(B) = (1/2)(1/6) = 1/12.

An example of a mutually exclusive event is the following. Consider a fair six-sided die as before, only in addition to the numbers 1 through 6 on each face, we have the property that the even-numbered faces are colored red, and the odd-numbered faces are colored green. Let event A be rolling a green face, and event B be rolling a 6. Then

P(B) = 1/6

P(A) = 1/2

as in our previous example. But it is obvious that events A and B cannot simultaneously occur, since rolling a 6 means the face is red, and rolling a green face means the number showing is odd. Therefore

P(A and B) = 0.

Therefore, we see that a mutually exclusive pair of nontrivial events are also necessarily dependent events. This makes sense because if A and B are mutually exclusive, then if A occurs, then B cannot also occur; and vice versa. This stands in contrast to saying the outcome of A does not affect the outcome of B, which is independence of events.

Amir
  • 15
  • 4
minerals
  • 378
  • 2
  • 12
20

Mutually exclusive event :- two events are mutually exclusive event when they cannot occur at the same time. e.g if we flip a coin it can only show a head OR a tail, not both.

Independent event :- the occurrence of one event does not affect the occurrence of the others e.g if we flip a coin two times, the first time may show a head, but this does not guarantee that the next time when we flip the coin the outcome will also be heads. From this example we can see the first event does not affect the occurrence of the next event.

ilovemy
  • 3
  • 4
Obaidullah Habibi
  • 201
  • 2
  • 2
  • This characterisation of independence of events should perhaps be fine-tuned: flipping a coin twice, the events {HH,HT} and {HT,TH} are independent, yet if the first event occurs, the second event can no longer occur via outcome TH so its “occurrence” is in a sense affected. I wrote more in my [Answer](https://math.stackexchange.com/a/4419308/21813) just posted. – ryang Apr 03 '22 at 12:26
7

If I toss a coin twice, the result of the first toss and the second toss are independent.

However the event that you get two heads is mutually exclusive to the event that you get two tails.

Suppose two events have a non-zero chance of occurring.

Then if the two events are mutually exclusive, they can not be independent.

If two events are independent, they cannot be mutually exclusive.

NNOX Apps
  • 1
  • 15
  • 118
  • 216
copper.hat
  • 161,568
  • 8
  • 96
  • 225
4

This question already has very good answers, I'm gonna add a visualization for independents events using some special diagrams. In these diagrams proportion of events to sample space represents their probability. Our sample space is a rectangle of 9x5 = 45 units:

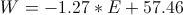
enter image description here

We have event A (3x5) so P(A) = 3x5/9x5 = 15/45 = 1/3:

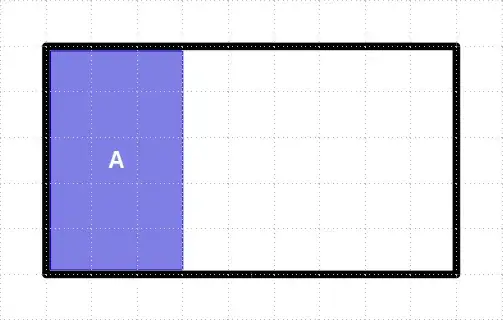
enter image description here

And event B (9x3) so P(B) = 9x3/9x5 = 27/45 = 3/5:

enter image description here

These two events intersect as:

enter image description here

∩ occupies 3x3 units:

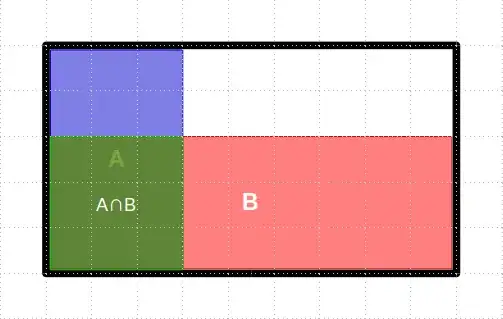
enter image description here

(∣) = (∩) / () so (∣) = 9/27 = 1/3. But this is same as P(A)!

enter image description here

and (∣) = (∩) / () so (∣) = 9/15 = 3/5. But this is same as P()!

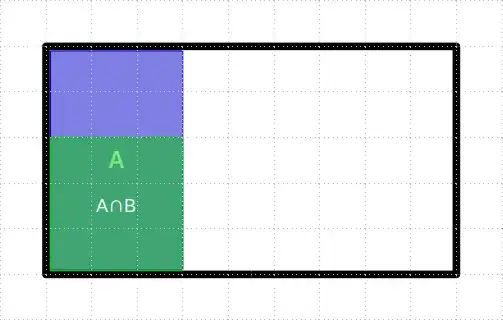
enter image description here

As in the two last diagrams, occurrence of one event doesn't affect the probability of the other event, these two events are called independent. So knowledge about occurrence of one of them doesn't affect our knowledge about probability of the other one. But this is not because they have nothing in common, on the contrary they are kinda in harmony by wiping out (the given event reduces sample space to itself, so it wipes out its complement) sample space in such a way that the other event proportion to given event doesn't change. I'd like to remember them as perpendicular events.

Xaqron
  • 311
  • 2
  • 12
1

Events are Independent when happening of one does not influence happening of other. Eruption of volcano on Earth and orbit of Mars do not influence each other, so are independent events.

Growth of human population and preservation of many other species are mutually exclusive, as the one can only happen if the other does not happen.

Strictly speaking, mutually exclusive does not imply that one of them must happen. If there is a large asteroid impact on Earth, then neither human population grows nor endangered species are preserved.

akhil999in
  • 29
  • 1
0

It will be easier if we distinguish "mutually exclusiveness" from "independency" by considering the sample space in mind.

  • Two events that are compared for mutually exclusiveness must be from a single sample space. For example,

    • Tossing a coin twice. $A=\{HH\}$ is an event in which the head shows up twice and $B=\{TT\}$ is an event in which the tail shows up twice. Their share the same sample space $S=\{HH,HT,TH,TT\}$. As $A\cap B=\{\}$, they are mutually exclusive.

  • Two events that are compared for independency must be from two sample spaces. For example,

    • Tossing a coin twice. $A=\{H\}$ is an event in which the head shows up in the first throw and $B=\{T\}$ is an event in which the tail shows up in the second throw. The sample space for the first trial is $S_1=\{H,T\}$ and the sample space for the second trial is $S_2=\{H,T\}$ As $S_1=S_2$, they are independent.

The next additional questions are "is it possible to have 2 events that are"

  • "both mutually exclusive and independent?"

  • "both mutually exclusive and dependent?"

I will update this answer in the future to answer the additional questions above.

Intellectual Gymnastics Lover
  • 1
  • 10
  • 23
  • 2
    Your answer is wrong, an event could be: The first coin is head and the other the second coin is tail (A'={HH,HT},B'={TT,HT}) and are from the same space. They are independent (P(A'|B')=P(A'&B')/P(B')=1/2=P(A')) while two heads (A) and two tails (B) are exclusive (P(A&B)=0) – Ernesto Iglesias Jan 26 '21 at 17:32
0

Let $A$ be the event of hitting a dartboard's bullseye, and $B$ be the event of hitting within its inner ring.

  1. Are these definitions correct?

    Two events are mutually exclusive if they can't both happen.

    False: Events $A$ and $B$ are mutually exclusive $\Big(P(A\cap B)=P(A)=0\Big),$ yet do happen simultaneously.

    Definition: Two events are mutually exclusive if they almost never or never both happen, that is, if their joint probability is zero.

  2. Independent events are events where knowledge of the probability of one doesn't change the probability of the other.

    False: Events $A$ and $B$ are independent $\Big(P(A\cap B)=P(A)=0=P(A)\,P(B)\Big),$ yet the knowledge that $A$ occurs increases $B$'s probability to $1.$

    A more literal-minded counterexample: landing Heads and landing Tails are dependent events $\Big(P(A\cap B)=0\ne\frac14=P(A)\,P(B)\Big),$ yet knowledge of the former's probability does change the latter's probability.

    Informal characterisation: Two events, at least one of which has a positive probability, are independent if the knowledge that one happens doesn't change the other's probability.

    Definition: Events $X$ and $Y$ are independent if $\,P(X\cap Y)=P(X)\,P(Y).$

  3. Is there any connection between independent events and mutually exclusive events?

    Let $X$ and $Y$ be positive-probability events. If $X$ and $Y$ are mutually exclusive, then $P(X\cap Y)=0;$ since $P(X)\,P(Y)>0,$ we have that $P(X\cap Y)\ne P(X)\,P(Y),$ that is, $X$ and $Y$ are dependent.

    Intuitively: if $X$ and $Y$ are mutually exclusive, then they almost never or never both happen; thus, knowing that event $Y$ happens means knowing that event $X$ almost doesn't or doesn't happen; so, knowing that $Y$ happens decreases $X$'s probability to zero; that is, events $X$ and $Y$ are dependent.

    Be careful though: events $A$ and $B$ above are mutually exclusive but independent, while the events {landing $'3'$ in a die roll} and {landing an odd number in a die roll} are dependent although not mutually exclusive.

ryang
  • 23,757
  • 12
  • 62
  • 142