How to prove that $\lim\limits_{x\to0}\frac{\sin x}x=1$?

Question

How can one prove the statement $$\lim_{x\to 0}\frac{\sin x}x=1$$ without using the Taylor series of $\sin$, $\cos$ and $\tan$? Best would be a geometrical solution.

This is homework. In my math class, we are about to prove that $\sin$ is continuous. We found out, that proving the above statement is enough for proving the continuity of $\sin$, but I can't find out how. Any help is appreciated.

Answer 1

The area of $\triangle ABC$ is $\frac{1}{2}\sin(x)$. The area of the colored wedge is $\frac{1}{2}x$, and the area of $\triangle ABD$ is $\frac{1}{2}\tan(x)$. By inclusion, we get $$ \frac{1}{2}\tan(x)\ge\frac{1}{2}x\ge\frac{1}{2}\sin(x)\tag{1} $$ Dividing $(1)$ by $\frac{1}{2}\sin(x)$ and taking reciprocals, we get $$ \cos(x)\le\frac{\sin(x)}{x}\le1\tag{2} $$ Since $\frac{\sin(x)}{x}$ and $\cos(x)$ are even functions, $(2)$ is valid for any non-zero $x$ between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$. Furthermore, since $\cos(x)$ is continuous near $0$ and $\cos(0) = 1$, we get that $$ \lim_{x\to0}\frac{\sin(x)}{x}=1\tag{3} $$ Also, dividing $(2)$ by $\cos(x)$, we get that $$ 1\le\frac{\tan(x)}{x}\le\sec(x)\tag{4} $$ Since $\sec(x)$ is continuous near $0$ and $\sec(0) = 1$, we get that $$ \lim_{x\to0}\frac{\tan(x)}{x}=1\tag{5} $$

Answer 2

You should first prove that for $x > 0$ small that $\sin x < x < \tan x$. Then, dividing by $x$ you get $$ { \sin x \over x} < 1 $$ and rearranging $1 < {\tan x \over x} = {\sin x \over x \cos x }$ $$ \cos x < {\sin x \over x}. $$ Taking $x \rightarrow 0^+$ you apply the squeeze theorem. For $x < 0$ and small use that $\sin(-x) = -\sin x$ so that $${\sin(-x) \over -x} = {\sin x \over x}.$$ As far as why the first inequality I said is true, you can do this completely from triangles but I don't know how to draw the pictures here.

Answer 3

Usually calculus textbooks do this using geometric arguments followed by squeezing.

Here's an Euler-esque way of looking at it---not a "proof" as that term is usually understood today, but still worth knowing about.

Let $\theta$ be the length of an arc along the circle of unit radius centered at $(0,0)$, from the point $(1,0)$ in a counterclockwise direction to some point $(\cos\theta,\sin\theta)$ on the circle. Then of course $\sin\theta$ is the height of the latter point above the $x$-axis. Now imagine what happens if $\theta$ is an infinitely small positive number. Then the arc is just an infinitely short vertical line, and the height of the endpoint above the $x$-axis is just the length of the arc. I.e. when $\theta$ is an infinitely small number, then $\sin\theta$ is the same as $\theta$. It follows that when $\theta$ is an infinitely small nonzero number, then $\dfrac{\sin\theta}{\theta}=1$.

That is how Euler viewed the matter. See his book on differential calculus.

Answer 4

Look at this link:

http://fatosmatematicos.blogspot.com/2010/08/provas-sem-palavras-parte-20.html

Here is the picture I copied from that blog:

Answer 5

I am not sure if it counts as proof, but I have seen this done by a High Schooler.

In the given picture above, $\displaystyle 2n \text{ EJ} = 2nR \sin\left( \frac{\pi}{n } \right ) = \text{ perimeter of polygon }$.

$\displaystyle \lim_{n\to \infty }2nR \sin\left( \frac{\pi}{n } \right ) = \lim_{n\to \infty } (\text{ perimeter of polygon }) = 2 \pi R \implies \lim_{n\to \infty}\frac{\sin\left( \frac{\pi}{n } \right )}{\left( \frac{\pi}{n } \right )} = 1$ and let $\frac{\pi}{n} = x$.

Answer 6

I claim that for $0<x<\pi/2$ that the following holds $$\sin x \lt x \lt \tan x$$
In the diagram, we let $OC=OA=1$. In other words, $Arc\:CA=x$ is an arc of a unit circle. The shortest distance from point $C$ to line $AO$ is line $CE=\sin x$ (because $CE\perp OA$). Another path from point $C$ to line $OA$ is arc $CA$ (which is longer than CE because it is not the shortest path). So we have at the very least $$\sin x \lt x$$ Now we need to show that line $BA=\tan x \gt x$.
Lines $AD$ and $CD$ are both tangent to arc $CA$. $CD+DA$ is longer than arc $CA$ because the set of points bound by sector $OCA$ is a subset of the set of points bound by quadrilateral $OCDA$, both of which are convex sets. This means that the perimeter of quadrilateral $OCDA$ must be longer than the perimeter of the sector $OCA$ (as per Archimedes, On the Sphere and Cylinder Book I). But both the sector and the quadrilateral both have sides $OC$ and $OA$, so we have $$CA=x<DC+DA$$ But $BD>CD$ because it is the hypotenuse in $\triangle BCD$ we have $$\tan x = BA = BD+DA\gt CD+DA \gt CA=x \gt \sin x$$

So we have $$\sin x \lt x \lt \tan x$$ $$\frac{\sin x}{x} \lt 1 \lt \frac{\tan x}{x}=\frac{\sin x}{x}\cdot\sec x$$ From this we can extract $$\frac{\sin x}{x} \lt 1$$ and $$1 \lt \frac{\sin x}{x}\cdot\sec x$$ $$\cos x \lt \frac{\sin x}{x}$$ Putting these inequalities back together we have $$\cos x \lt \frac{\sin x}{x} \lt 1$$

Because $\displaystyle\lim_{x\to 0}\cos x = 1$, by the squeeze theorem we have $$\lim_{x\to 0}\frac{\sin x}{x}=1$$

Answer 7

Here you may see an elementary approach that starts from a very interesting result, see this problem. All you need is a bit of imagination. When we take $\lim_{n\rightarrow\infty} \frac{n\sin(\frac{\pi}{n})}{1+\sin(\frac{\pi}{n})}$ we may notice that we have infinitely many circles surrounding the unit circle with infinitely small diameters that lastly perfectly approximate the length of the unit circle when having it there infinity times . Therefore when multiplying n by the radius under the limit to infinity we get π. Let's denote $\frac{\pi}{n}$ by x.

$$\lim_{x\rightarrow0}\frac{\pi\sin(x)}{x(1+\sin(x))}={\pi}\Rightarrow\lim_{x\rightarrow0}\frac{\sin(x)}{x(1+\sin(x))}=1\Rightarrow\lim_{x\rightarrow0}\frac{\sin(x)}{x}=1$$

The proof is complete.

Answer 8

Don't you feel strange about why most of the proofs are done with a figure? I've had this problem in the beginning, and realized after that this is due to the definition we use for the function $\sin x$. Because the usual definition of $\sin x$ we all study first in high schools depends on “classical geometry” and usually with a figure, you should depict out the figure and to make it clear.

However, if you use other definitions of $\sin x$ that are equivalent to the former, you'll find it more simple. For example,

$$\sin x = \frac{x^1}{1!} - \frac{x^3}{3!}+ \frac{x^5}{5!} - \cdots + \cdots - \cdots$$

and hence

$$\frac{\sin x}x = \frac{x^0}{1!} - \frac{x^2}{3!}+ \frac{x^4}{5!} - \cdots$$

which obviously tends to $1$ as $x$ approaches 0.

Answer 9

Here's one more: $$ \lim_{x \to 0} \frac{\sin x}{x}=\lim_{x \to 0} \lim_{v \to 0}\frac{\sin (x+v)-\sin v}{x}\\ =\lim_{v \to 0} \lim_{x \to 0}\frac{\sin (x+v)-\sin v}{x}=\lim_{v \to 0}\sin'v=\lim_{v\ \to 0} \cos v=1 $$

Answer 10

It depends on your definition of the sine function. I would suggest checking out the geometric proof in ProofWiki.

Answer 11

The strategy is to find $\frac{d\arcsin y}{dy}$ first. This can easily be done using the picture below.

From the above picture, $\arcsin y$ is twice the area of the orange bit. The area of the red bit is ${1 \over 2}y\sqrt{1-y^2}$. The area of the red bit plus the orange bit is $\int_{0}^y \sqrt{1-Y^2} dY$. So $$\arcsin y = 2\int_{0}^y \sqrt{1-Y^2} dY - y\sqrt{1-y^2}.$$ Differentiating with respect to $y$ gives $\frac{d\arcsin y}{dy} = \frac{1}{\sqrt{1-y^2}}$. Using the theorem for the derivative of inverse functions yields $\sin' \theta = \sqrt{1 - \sin^2 \theta} = \cos \theta$.

(A similar thing can be done with the arc length definition of $\arcsin$.)

Answer 12

Here is a different approach that uses the integral definition of the arcsine function. We will deduce the limit of interest without appeal to geometry or differential calculus.

Instead, we only rely on elementary analysis of continuous functions and their inverses along with simple properties of the Riemann integral. To that end, we now proceed.

---

We define the sine function, $\sin(x)$, as the inverse function of the function $f(x)$ given by

$$\bbox[5px,border:2px solid #C0A000]{f(x)=\int_0^x \frac{1}{\sqrt{1-t^2}}\,dt }\tag 1$$

for $|x|< 1$.

NOTE: It can be shown that the sine function defined as the inverse of $f(x)$ given in $(1)$ has all of the familiar properties that characterize the circular function $\sin(x)$.

It is straightforward to show that since $\frac{1}{\sqrt{1-t^2}}$ is positive and continuous for $t\in (-1,1)$, $f(x)$ is continuous and strictly increasing for $x\in (-1,1)$ with $\displaystyle\lim_{x\to 0}f(x)=f(0)=0$.

Therefore, since $f$ is continuous and strictly increasing, its inverse function, $\sin(x)$, exists and is also continuous and strictly increasing with $\displaystyle \lim_{x\to 0}\sin(x)=\sin(0)=0$.

---

From $(1)$, we have the bounds (SEE HERE)

$$\bbox[5px,border:2px solid #C0A000]{1 \le \frac{f(x)}x\le \frac{1}{\sqrt{1-x^2}}} \tag 2$$

for $x\in (-1,1)$, whence applying the squeeze theorem to $(2)$ yields

$$\lim_{x\to 0}\frac{f(x)}{x}=1 \tag 3$$

---

Finally, let $y=f(x)$ so that $x=\sin(y)$. As $x\to 0$, $y\to 0$ and we can write $(3)$ as

$$\lim_{y\to 0}\frac{y}{\sin(y)}=1$$

from which we have

$$\bbox[5px,border:2px solid #C0A000]{\lim_{y\to 0}\frac{\sin(y)}{y}=1}$$

as was to be shown!

---

NOTE:

We can deduce the following set of useful inequalities from $(2)$. We let $x=\sin(\theta)$ and restrict $x$ so that $x\in [0,1)$. In addition, we define new functions, $\cos(\theta)=\sqrt{1-\sin^2(\theta)}$ and $\tan(\theta)=\sin(\theta)/\cos(\theta)$.

Then, we have from $(2)$

$$\bbox[5px,border:2px solid #C0A000]{y\cos(y)\le \sin(y)\le y\le \tan(y)} $$

which are the familiar inequalities often introduced in an introductory geometry or trigonometry course.

Answer 13

Let $f:\{y\in\mathbb{R}:y\neq 0\}\to\mathbb{R}$ be a function defined by $f(x):=\dfrac{\sin x}{x}$ for all $x\in \{y\in\mathbb{R}:y\neq 0\}$.

We have $\displaystyle\lim_{x \to 0}\dfrac{\sin x}{x}=1$ if and only if for every $\varepsilon>0$, there exists a $\delta>0$ such that $|f(x)-1|<\varepsilon$ whenever $0<|x-0|<\delta$.

Let $\varepsilon>0$ be an arbitrary real number.

Note that $\sin x=\displaystyle \sum_{n=0}^{\infty}(-1)^n\dfrac{x^{2n+1}}{(2n+1)!}$.

If $x \neq 0$, we have $\dfrac{\sin x}{x}=$$\displaystyle \sum_{n=0}^{\infty}(-1)^n\dfrac{x^{2n}}{(2n+1)!}=1+$$\displaystyle \sum_{n=1}^{\infty}(-1)^n\dfrac{x^{2n}}{(2n+1)!}$.

We thus have

$|f(x)-1|=\left|\dfrac{\sin x}{x}-1\right|=\left|\displaystyle \sum_{n=1}^{\infty}(-1)^n\dfrac{x^{2n}}{(2n+1)!}\right|\leq \left|\displaystyle\sum_{n=1}^{\infty} \dfrac{x^{2n}}{(2n+1)!}\right|\leq \displaystyle\sum_{n=1}^{\infty} \left|\dfrac{x^{2n}}{(2n+1)!}\right|$

Therefore we have

$|f(x)-1|\leq \displaystyle\sum_{n=1}^{\infty} \left|\dfrac{x^{2n}}{(2n+1)!}\right|\leq \displaystyle \sum_{n=1}^{\infty} |x^{2n}|=\sum_{n=1}^{\infty}|x^2|^n$

If $0<|x|<1$, then $0<|x^2|<1$, and the infinite series $\displaystyle\sum_{n=1}^{\infty}|x^2|^n$ converges to $\dfrac{x^2}{1-x^2}$.

Choose $\delta:=\sqrt{\dfrac{\varepsilon}{1+\varepsilon}}$. Then $0<|x-0|<\delta$ implies that $0<|x|<$$\sqrt{\dfrac{\varepsilon}{1+\varepsilon}}<1$, and hence $x^2<\varepsilon-\varepsilon x^2$. But $x^2<\varepsilon-\varepsilon x^2$ implies that $\dfrac{x^2}{1-x^2}<\varepsilon$.

We therefore have $\sum_{n=1}^{\infty}|x^2|^n<\varepsilon$ whenever $0<|x-0|<\delta$. But since $|f(x)-1|\leq\displaystyle\sum_{n=1}^{\infty}|x^2|^n$, we have $|f(x)-1|<\varepsilon$ whenever $0<|x-0|<\delta$.

Since $\varepsilon$ was arbitrary, we have $\displaystyle\lim_{x \to 0}\dfrac{\sin x}{x}=1$.

Answer 14

Usual proofs can be circular, but there is a simple way for proving such inequality.

Let $\theta$ be an acute angle and let $O,A,B,C,D,C'$ as in the following diagram:

We may show that:

$$ CD \stackrel{(1)}{ \geq }\;\stackrel{\large\frown}{CB}\; \stackrel{(2)}{\geq } CB\,\stackrel{(3)}{\geq} AB $$

$(1)$: The quadrilateral $OCDC'$ and the circle sector delimited by $O,C,C'$ are two convex sets. Since the circle sector is a subset of the quadrilateral, the perimeter of the circle sector is less than the perimeter of the quadrilateral.

$(2)$: the $CB$ segment is the shortest path between $B$ and $C$.

$(3)$ $CAB$ is a right triangle, hence $CB\geq AB$ by the Pythagorean theorem.

In terms of $\theta$ we get: $$ \tan\theta \geq \theta \geq 2\sin\frac{\theta}{2} \geq \sin\theta $$ for any $\theta\in\left[0,\frac{\pi}{2}\right)$. Since the involved functions are odd functions the reverse inequality holds over $\left(-\frac{\pi}{2},0\right]$, and $\lim_{\theta\to 0}\frac{\sin\theta}{\theta}=1$ follows by squeezing.

---

A slightly different approach might be the following one: let us assume $\theta\in\left(0,\frac{\pi}{2}\right)$.
By $(2)$ and $(3)$ we have $$ \theta \geq 2\sin\frac{\theta}{2}\geq \sin\theta $$ hence the sequence $\{a_n\}_{n\geq 0}$ defined by $a_n = 2^n \sin\frac{\theta}{2^n}$ is increasing and bounded by $\theta$. Any increasing and bounded sequence is convergent, and we actually have $\lim_{n\to +\infty}a_n=\theta$ since $\stackrel{\large\frown}{BC}$ is a rectifiable curve and for every $n\geq 1$ the $a_n$ term is the length of a polygonal approximation of $\stackrel{\large\frown}{BC}$ through $2^{n-1}$ equal segments. In particular

$$ \forall \theta\in\left(0,\frac{\pi}{2}\right), \qquad \lim_{n\to +\infty}\frac{\sin\left(\frac{\theta}{2^n}\right)}{\frac{\theta}{2^n}} = 1 $$ and this grants that if the limit $\lim_{x\to 0}\frac{\sin x}{x}$ exists, it is $1$. By $\sin x\leq x$ we get $\limsup_{x\to 0}\frac{\sin x}{x}\leq 1$, hence it is enough to show that $\liminf_{x\to 0}\frac{\sin x}{x}\geq 1$. We already know that for any $x$ close enough to the origin the sequence $\frac{\sin x}{x},\frac{\sin(x/2)}{x/2},\frac{\sin(x/4)}{x/4},\ldots$ is convergent to $1$, hence we are done.

Long story short: $\lim_{x\to 0}\frac{\sin x}{x}=1$ follows from the fact that a circle is a rectifiable curve, and a circle is a rectifiable curve because it is the boundary of a convex, bounded subset of $\mathbb{R}^2$. The convexity of the disk follows from the triangle inequality: a disk is a closed ball for the euclidean distance.

---

$(1)$ relies on this powerful Lemma:

Lemma. If $A,B$ are convex bounded sets in $\mathbb{R}^2$ and $A\subsetneq B$, the perimeter of $A$ is less than the perimeter of $B$.

Proof: by boundedness and convexity, $\partial A$ and $\partial B$ are rectifiable, with lengths $L(A)=\mu(\partial A),\,L(B)=\mu(\partial B)$. Always by convexity, there is some chord in $B$ that does not meet the interior of $A$ (a tangent to $\partial A$ at a smooth point does the job, for instance). Assume that such chord has endpoints $B_1, B_2 \in \partial B$ and perform a cut along $B_1 B_2$: both the area and the perimeter of $B$ decrease, but $B$ remains a bounded convex set enclosing $A$. Since $A$ can be approximated through a sequence of consecutive cuts, $L(A)<L(B)$ follows.

Answer 15

Let $\sin(x)$ is defined as solution of $\frac{d^2}{dx^2}\textrm{f}(x)=-\textrm{f}(x)$ with $\mathrm f(0)=0,\,\frac{d}{dx}\mathrm f(0)=C$ initial conditions, so exact solution is $\mathrm f(x)=C\cdot\sin(x)$. Define second derivative as $$ \begin{align*} \frac{d^2}{dx^2}\textrm{f}(x)=\lim_{\Delta x\to 0}{\frac{\frac{\mathrm f(x)-\mathrm f(x-\Delta x)}{\Delta x}-\frac{\mathrm f(x-\Delta x)-\mathrm f(x-2\cdot\Delta x)}{\Delta x}}{\Delta x}}&=\\=\lim_{\Delta x\to 0}{\frac{\mathrm f(x)-2\cdot \mathrm f(x-\Delta x)+\mathrm f(x-2\cdot\Delta x)}{\Delta x^2}} \end{align*} $$ we can easy check this limit for any (?) functions. Similarly, we can define the first derivative for right, middle and left points: $$ \frac{d}{dx}\textrm{f}(x)\left\{ \begin{aligned} &=\lim_{\Delta x\to 0}{\frac{\mathrm f(x)-\mathrm f(x-\Delta x)}{\Delta x}} \\ &=\lim_{\Delta x\to 0}{\frac{\mathrm f(x-\Delta x)-\mathrm f(x-2\cdot\Delta x)}{\Delta x}}\\ &=\lim_{\Delta x\to 0}{\frac{\mathrm f(x)-\mathrm f(x-2\cdot\Delta x)}{2\cdot\Delta x}} \end{aligned} \right. $$ Let's use the finite elements method assuming $Td=\Delta x,\,y_n=\mathrm f(x),\,y_{n-1}=\mathrm f(x-\Delta x),\,y_{n-2}=\mathrm f(x-2\cdot \Delta x)$ Override differential equation as $$ \frac{y_n-2\cdot y_{n-1}+y_{n-2}}{Td^2}=-y_n $$ Now solve this implicit equation for $y_n$ to obtain explicit recurrence relation: $$ y_n = \frac{2\cdot y_{n-1}-y_{n-2}}{1+Td^2} $$ Using arbitrarily small but non-zero quantity Td we can plot exponentially decaying sampled sine function (because the poles are inside the unit circle of the transfer function corresponding to the given recurrence relation). Similarly we write three systems for the initial conditions:

$$ \left\{ \begin{aligned} &y_n = \frac{2\cdot y_{n-1}-y_{n-2}}{1+Td^2} \\ &C=\frac{y_n-y_{n-1}}{Td} \end{aligned}\right. $$ $$ \left\{ \begin{aligned} &y_n = \frac{2\cdot y_{n-1}-y_{n-2}}{1+Td^2} \\ &C=\frac{y_{n-1}-y_{n-2}}{Td} \end{aligned}\right. $$ $$ \left\{ \begin{aligned} &y_n = \frac{2\cdot y_{n-1}-y_{n-2}}{1+Td^2} \\ &C=\frac{y_n-y_{n-2}}{2\cdot Td} \end{aligned}\right. $$ Solve this sequence of equations for $y_{n-1}$ and $y_{n-2}$: $$ \left\{ \begin{aligned} &y_{n-1} = -C\cdot Td + y_{n}\\ &y_{n-2}=-2\cdot C\cdot Td + y_{n}\cdot\left(1-Td^2\right)\ \end{aligned}\right. $$ $$ \left\{ \begin{aligned} &y_{n-1} = -C\cdot Td + y_{n}\cdot\left(1+Td^2\right)\\ &y_{n-2}=-2\cdot C\cdot Td + y_{n}\cdot\left(1+Td^2\right)\ \end{aligned}\right. $$ $$ \left\{ \begin{aligned} &y_{n-1} = -C\cdot Td + y_{n}\cdot\left(1+\frac{Td^2}{2}\right)\\ &y_{n-2}=-2\cdot C\cdot Td + y_{n}\ \end{aligned}\right. $$ At zero point $y_n=\mathrm f(0)=0$ and we can see linear dependence: $$ \begin{aligned} &y_{n-1} = -C\cdot Td\\ &y_{n-2}=-2\cdot C\cdot Td \end{aligned} $$ for all three solutions. Replace back: $$ \begin{array}{l} \mathrm f(0)&=0\\ \mathrm f(0-\Delta x) &= -C\cdot \Delta x\\ \mathrm f(0-2\cdot \Delta x) &= -2\cdot C\cdot \Delta x \end{array} $$ So all three $\frac{d}{dx}\mathrm f(0)$ limits is equal to $C$ at $x=0$ and in accordance with $\mathrm f(x)=C\cdot\sin(x)$ by definition we can write $$ \lim_{\Delta x\to 0}{\frac{\mathrm f(0)-\mathrm f(0-\Delta x)}{\Delta x}}=\lim_{\Delta x\to 0}{\frac{0-(-C \cdot \Delta x)}{\Delta x}}=C $$ Thus $$ \lim_{\Delta x\to 0}{\frac{\sin(0)-C\cdot\sin(0-\Delta x)}{\Delta x}}=\lim_{\Delta x\to 0}{\frac{C\cdot\sin(\Delta x)}{\Delta x}}=C\cdot\lim_{\Delta x\to 0}{\frac{\sin(\Delta x)}{\Delta x}}=C $$ and $\lim_{\Delta x\to 0}{\frac{\sin(\Delta x)}{\Delta x}}=1$

Answer 16

Simple one is using sandwich theorem Which demonstrated earlier.In this method you have to show that $\frac{\sin x}{x} $ lies between other two functions. As $x \longrightarrow 0$ both of them will tends to ONE.

Then as in the case of sandwich (if both the bread part go to one stomach the middle portion will also go to the same stomach) $\frac{\sin x}{x}$ will go to ONE.

You can use geogebra to see the visualization of this phenomena using geogebra.First you input $\sin x$ and $x$ and observe that near to $0$ values of $\sin x$ and $x$ are same.

Secondly input $\frac{\sin x}{x}$ then observe function is approaching to $1$ as $x$ tends to $0$

Answer 17

Originally posted on the proofs without words post, here is a simple image that explains the derivative of $\sin(x)$, which as we all know, is directly related to the limit at hand.

If one is not so convinced, take a look at the above picture and notice that if $u\pm h$ is in the first quadrant, then

$$\frac{\sin(x+h)-\sin(x)}h<\cos(x)<\frac{\sin(x-h)-\sin(x)}{-h}$$

---

Notice that

$$ \begin{align}\frac{d}{dx}\sin(x)&=\lim_{h\to0}\frac{\sin(x+h)-\sin(x)}h\\\text{picture above}&=\lim_{h\to0}\frac{\sin(x)\cos(h)+\cos(x)\sin(h)-\sin(x)}h\\\cos(x)&=\lim_{h\to0}\sin(x)\frac{\cos(h)-1}h+\cos(x)\frac{\sin(h)}h\\\cos(0)&=\lim_{h\to0}\frac{\sin(h)}h\end{align} $$

Answer 18

The answer ultimately depends on how you define $\sin x$ in the first place.

Here is a more fun one! $\sin x$ is the unique function satisfying $$ y'' = -y; y(0)=0, y'(0)=1 $$ By Theory of Ordinary Differential Equations a unique function defined on some interval containing $0$ exists. Now that we called it $\sin x$, we see that $$ \frac{\sin x}{x} = \frac{\sin x - \sin 0}{x - 0} \to y'(0) = 1 \ ,$$ by definition of derivative at $x=0$ and the initial conditions defining $y(x)=\sin x \ .$

Answer 19

Here is another approach.

(1) (2)

In the large triangle, $$\tan(\theta)=\frac{opp}{adg}=\frac{z}{1}=z$$ So the triangle has height $$z=\tan(\theta)$$ and base $1$ so it's area is $$Area(big triangle)=\frac{1}{2}z=\frac{1}{2}\tan(\theta)$$

Next the sector area as a fraction of the entire circle, the sector is (see the right hand side of picture (1))$$\frac{\theta}{2\pi}$$ of the entire circle so it's area is

$$Area(sector)=\frac{\theta}{2\pi}*(\pi)(1)^2=\frac{\theta}{2}$$ The triangle within the sector has height $y$. But $y=\frac{y}{1}=\frac{opp}{hyp}=\sin(\theta)$ so the small triangle has height $y=\sin(\theta)$ and base $1$ so its area is $$Area(small triangle)=\frac{1}{2}y=\frac{1}{2}\sin(\theta)$$ Now we can use the sandwich theorem as $$Area(big triangle)\geq Area(sector)\geq Area(small triangle)$$

using the equations we worked out above this becomes

$$\frac{\tan(\theta)}{2}\geq\frac{\theta}{2}\geq\frac{\sin(\theta)}{2}$$ now multipliying through by two and using the fact that $$\tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$$ we get that $$\frac{\sin(\theta)}{\cos(\theta)}\geq\theta\geq\sin(\theta)$$ taking reciprocals changes the inequalities so we have that $$\frac{\cos(\theta)}{\sin(\theta)}\leq\frac{1}{\theta}\leq\frac{1}{\sin(\theta)}$$ now finally multiplying through by $\sin(\theta)$ we get $$\cos(\theta)\leq\frac{\sin(\theta)}{\theta}\leq1$$ Now $$\lim \limits_{\theta \to 0}\cos(\theta)=1$$ and$$\lim \limits_{\theta \to 0}1=1$$

so by the sandwhich theorem $$\lim \limits_{\theta \to 0}\frac{\sin(\theta)}{\theta}=1$$ also. QED

Answer 20

How about this proof?

We can check that function defined as \begin{align} \int_{-m}^m e^{2\pi i k x} \mathrm{d}{k} \end{align} is continuous and have a value $2m$ at $x=0$.

It is same with \begin{align} \int_{-m}^m e^{2\pi i k x} \mathrm{d}{k} = \dfrac{e^{2\pi i m x} - e^{-2\pi i m x}}{2\pi i x} = \dfrac{\sin 2 \pi m x}{\pi x} \end{align}

In conclusion, \begin{align} \lim_{x \to 0}\dfrac{\sin 2 \pi m x}{\pi x} = \lim_{x \to 0}\int_{-m}^m e^{2\pi i k x} \mathrm{d}{k} = 2m \end{align}

You can adjust $m$ as what you want.

Answer 21

For completeness answers let me suggest axiomatic approach to $\sin$ and $\cos$. One possible definition is here. I find another one(Ilyin, Poznyak: Fundamentals of Mathematical Analysis, 2005, vol.1, pages 146-155, Russian lang.), which claims, that there is only one pair of continuous functions on $\mathbb{R}$ for which fulfill

$$S(x+y)=S(x)C(y)+S(y)C(x)$$ $$C(x+y)=C(x)C(y)-S(y)C(x)$$ $$S^2(x)+C^2(x)=1$$ $$S(0)=0,S\left(\frac{\pi}{2}\right)=1,C(0)=1,C\left(\frac{\pi}{2}\right)=0$$ From this axioms can be obtained monotonic properties and can be proved, particularly, that for $x \in (0, \frac{\pi}{2})$ holds $0<S(x)<x< \frac{S(x)}{C(x)}$. Using last is easy to obtain $$\lim_{x \to 0}\frac{S(x)}{x}=1$$

Answer 22

This is a variant of robjohn's answer. The area of the sector $ADE$ is $\frac{1}{2}x\cos^2(x)$; the area of the triangle $ABC$ is $\frac{1}{2}\sin(x)$; and the area of the sector $ABC$ is $\frac{1}{2}x$. By inclusion, we find that for $0<x < \frac{\pi}{2}$, $$ \frac{1}{2}x\cos^2(x) \le \frac{1}{2}\sin(x) \le \frac{1}{2}x \, . $$ If we multiply each term in this inequality by $\frac{2}{x}$, we obtain the necessary bounds to apply the squeeze theorem: $$ \cos^2(x) \le \frac{\sin(x)}{x} \le 1 \, . $$ This inequality is also valid for $-\frac{\pi}{2} < x < 0$, as all three functions in the inequality are even.

Since $\cos$ is continuous at $0$, and $(\cdot)^2$ is continuous at $\cos(0)$, the function $x\mapsto \cos^2(x)$ is continuous at $0$, i.e. $$ \lim_{x \to 0}\cos^2(x)=1 \, . $$ Therefore, by the squeeze theorem, $$\lim_{x \to 0}\frac{\sin(x)}{x}=1 \, .$$

Answer 23

This is a new post on an old saw because this is one of those things where that I can see how that, all too sadly, the way in which we've structured the current maths curriculum really doesn't make it possible to do these kinds of things the justice they deserve and I think, ultimately, that is a disservice to many learners.

The truth is, this limit cannot really be given an honest proof without an honest definition of the sine function, first. And that is not as easy as it seems. Even if we consider the simple notion from many trigonometric treatments that the sine is equal to the "length of the opposite side of the right triangle divided by the length of its hypotenuse", that doesn't truly solve the problem because there is actually a subtle missing element and that is that sine is not a function of a "right triangle" (though you could define that if you wanted, and it'd be easy!), but of an angle measure. And actually parsing out what "angle measure" means, it turns out, is essentially equivalent to defining the sine function in the first place, so this approach is circular! (pun observed after writing despite not being originally intended!)

So how do we define sine, or angle measure? Unfortunately, any approach to this is such that it must involve calculus. This is because the angle measure we use is "smooth and steady", meaning that, basically, if we have some angle, we'd like fractionating that angle measure to fractionate the angle in the same manner as cutting up pieces of a pie: if I have an angle with the given angle measure $\theta$, then for the measure system to work I should be able to then produce an angle with measure $\frac{\theta}{n}$, should be an angle that is geometrically the $n$-section of the angle into $n$ congruent smaller angles that add up to the full angle.

Yet already, we can see right there that this is not trivial: consider $n = 3$. Then we have the famous "impossible" problem of "trisection of the angle" which vexed even the ancient Greeks and for which people would keep trying to pound at until Pierre Wantzel finally proved it undoable over two thousand years after. We are asking for a mathematical widget that can not only trisect, but 5-sect, 629-sect, etc. angles and in a systematic manner to boot!

Indeed, not only is the sine function not trivial, we could argue that even the exponential function is considerably easier to treat than sine, though I won't give such a treatment here.

Thus, how do we do it? Well, the key observation is that our "steady" angle measure is one which is, effectively, defined by the arc length of a segment of circle intercepted by the angle when drawn at the circle's center and projected outward. In particular, this should be "obvious" from the (circularly-introduced) geometric formula

$$\mbox{Length of circular arc} = r\theta$$

Since this is only a trivial multiplication, all the nontriviality must be in either defining $\theta$ in terms of geometric angles formed by lines, or in terms of defining the "length of a circular arc" and, moreover, these two problems must be equally hard. Hence, we will begin with the arc question first and one will see that this answer will end up using a fair bit of Calculus II material to answer this Calculus I-level question about a supposedly pre-Calculus mathematical object. Indeed, this is what the whole "radian measure" is: it's a measure of angles in terms of the arc length of the piece they cut from a unit circle (i.e. $r = 1$). "Degrees", are then just a weird multiple unit of actual length, equal to $\frac{2\pi}{360}$ (or better, $\frac{\tau}{360}$) of some other unit length.

If you use a somewhat more honest Trigonometry book, you will see something to the effect that sine and cosine are defined as basically being the coordinates on a unit circle when an angle measure $\theta$ has been emplaced from the $x$-axis:

$$C(\theta) := (\cos(\theta), \sin(\theta))$$

Now as said above, $\theta$ is arc length. Thus, what we have above is something called an arc length parameterization of the circle - and that tells us how we need to proceed. First, we need a separate definition of the arc length of a circle.

How do we get that? Well, we will obviously need a more elementary circle equation, first, than the one we just gave, and that means going to the simple algebraic definition,

$$x^2 + y^2 = 1$$

so that now we can solve using good ole' Algebra for $x$ and $y$ in at least a semicircle:

$$x(y) = \sqrt{1 - y^2}$$ $$y(x) = \sqrt{1 - x^2}$$

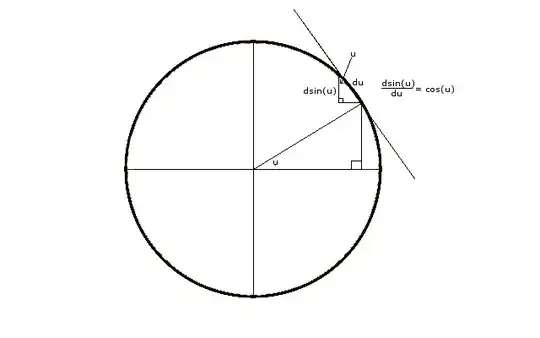
And now this is where we then must introduce Calculus II-level concept - namely, integration for arc length. The arc length swept between two values of the $x$-coordinate, for a curve given with $y$ as a function of $x$, is

$$\mbox{Arc Length}(x_1, x_2) := \int_{x_1}^{x_2} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} dx$$

Hence for the circle, now $\frac{dy}{dx} = \frac{1}{2} (1 - x^2)^{-1/2} \cdot (-2x) = \frac{-x}{\sqrt{1 - x^2}}$, so

$$\mbox{Arc Length}(x_1, x_2) = \int_{x_1}^{x_2} \sqrt{1 + \frac{x^2}{1 - x^2}} dx$$

which simplifies to

$$\mbox{Arc Length}(x_1, x_2) = \int_{x_1}^{x_2} \frac{1}{\sqrt{1 - x^2}} dx$$

Now, we use the Fundamental Theorem of Calculus to define the inverse sine as

$$\arcsin(x) := \int_{0}^{x} \frac{1}{\sqrt{1 - \xi^2}} d\xi$$

which is the arc length in terms of coordinate, and now the sine is its inverse, coordinate in terms of arc length:

$$\sin(\theta) := \arcsin^{-1}(\theta)$$

.

Finally, at this point, with a full, airtight definition of $\sin(x)$ now in hand, we are ready to evaluate the limit:

$$\lim_{x \rightarrow 0} \frac{\sin(x)}{x}$$

Since the "real", or base, function here is really the inverse function, i.e. $\arcsin$, we first proceed by making a change of variables: we consider instead the limit in terms of $y$ where $y(x) := \arcsin(x)$. Note that, trivially, $\arcsin(0) = 0$ from the integral definition, thus we get

$$\lim_{x \rightarrow 0} \frac{\sin(x)}{x} = \lim_{y \rightarrow 0} \frac{y}{\arcsin(y)}$$

Now for the right-hand limit, we need only consider the behavior of $\arcsin(y)$ when $y$ is small. Since the integrand, $\frac{1}{\sqrt{1 - x^2}}$, is differentiable at $x = 0$, it can be approximated with its tangent line (which really, should be also how we define tangent lines in the first place, as a "best approximation", a notion that can be done in an airtight, intuitive fashion through the use of a "zoom-in") and so likewise, the integral over a tiny sliver by integral of that same tangent line. By the power rule and chain rule,

$$\frac{d}{dx} \frac{1}{\sqrt{1 - x^2}} = \frac{d}{dx} (1 - x^2)^{-1/2} = \left(-\frac{1}{2}\right) (1 - x^2)^{-3/2} \cdot (-2x) = x(1 - x^2)^{3/2}$$

so the derivative at $x = 0$ is zero and the tangent line is horizontal: since also $\frac{1}{\sqrt{1 - x^2}}$ evaluated at $x = 0$ is $1$, the tangent is

$$T(x) := 1$$

hence

$$\int_{0}^{y} \frac{1}{\sqrt{1 - \xi^2}}\ d\xi \approx \int_{0}^{y} 1\ d\xi$$

when $y \approx 0$, and then the right-hand integral is approximately $y$, hence $\arcsin(y) \approx y$ when $y \approx 0$ and

$$\lim_{y \rightarrow 0} \frac{y}{\arcsin(y)} = \lim_{y \rightarrow 0} \frac{y}{y} = \lim_{y \rightarrow 0} 1 = 1$$

hence

$$\lim_{x \rightarrow 0} \frac{\sin(x)}{x} = 1$$

QED.

Nonetheless, as I mentioned before, this doesn't solve the requirements of the question which, while I'm sure its original asker has long moved on is, nonetheless, still relevant to calculus student after calculus student up to today: prove the limit using only Calculus I/pre-Calculus methods. What I am saying is that, in fact, that is not truly honestly possible and reveals a weakness of the curriculum in that it doesn't actually follow the proper logical buildup of the mathematical edifice.

What really should be done is to leave trig for later, that is, skip trig and go for Calculus first. When I studied maths on my own, I did just that. In fact, I'd say, as many educators have suggested, that most people don't need either, but really need more statistics instead. Then for those who do pursue higher maths, if we've done algebra and statistics, we already have right there a lot of interesting material we can build on for calculus, including the exponential function. There is no need to add trig functions to "sweeten the mix" when it's already plenty sweet with integrals of algebraic functions like $x \mapsto \sqrt{1 - x^2}$ which is a very nice example of the area-integration relation, and such can, if emphasized more heavily, potentially invite more nuanced thinking about integrals beside just "plugging and chugging integration rules". In particular, with a more limited set of functions, we can think about other ways we might approach them like just that and/or a variety of ways to interpret the integral which can only be good, I'd think, to develop more creative thinking about problems and less drilling in methods with little real understanding gained (and rote crunching integrals is even less relevant now with computer algebra software; more important is really being able to understand a problem and how its parts fit together and lead to a solution. That said, rote crunching is not something I suggest banning either but I suggest that ideas, concepts, and creativity should come first, then you get into those techniques because very often they are also still useful in analysis and being fluent at them can also make you able to solve problems more quickly, e.g. you don't want to be hitting up your calculator for 2+3 all the time in grade school and you don't want to be hitting up your CAS all the time to integrate $x \mapsto x^2$). On top of that, we have effectively now two different functions - logarithm and trigonometry - which we define by integrals, which means also that we can consider that we don't have to stop there, and this exposes the artificiality of the sacredness of so-called "elementary functions" and alows us to also perhaps consider a few more artifices of that sort like $\mathrm{erf}(x)$ which seems not too much more difficult but instead we simply reply that

$$\int e^{-x^2}\ dx$$

"can't be done" which, in light of having seen such things early on, feels like another sore cheat/blemish on the curriculum.

And to finish it all off - if you say calc can't be done before trig, I'd say that too bad Archimedes isn't here, as he would probably not have shared your sentiment since in fact he was one of the earliest to develop even a partial concept of integration and not only that but one of his applications of it was precisely the delineation of the arc length of a circle: that is why $\pi$ is called Archimedes' constant.

Answer 24

We can also use Euler's formula to prove the limit:

$$e^{ix} = \cos x + i\sin x$$

$$\lim_{x\to 0}\dfrac{\sin x}{x} = \implies \lim_{x\to 0} \dfrac{e^{ix}- e^{-ix}}{2i x}$$

$$= \lim_{x\to 0} \dfrac{e^{2ix}-1}{2ix}\times\dfrac 1{ e^{ix} }= 1 \times 1 = 1$$

since:

$\lim_{f(x)\to 0}\dfrac{e^{f(x)}-1}{f(x)} = 1$

Answer 25

Here is a proof to those familiar with power series.

The definition of $\sin(x)$ is

$$\sin(x) = \sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!}h^{2k+1}$$

Therefore we get

$$\begin{align} \lim_{x \to 0} \frac{\sin(x)}{x} &= \lim_{x \to 0} \frac{\sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!}x^{2k+1}}{x} \\&= \lim_{x \to 0} \sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!} x^{2k} \\&= 1 + \lim_{x \to 0} \sum_{k=1}^\infty \frac{(-1)^k}{(2k+1)!} x^{2k} \\&= 1 \end{align}$$

where we have used the fact that the power series $\sum_{k=1}^\infty \frac{(-1)^k}{(2k+1)!} x^{2k}$ has radius of convergence $R=\infty$ and therefore is continuous on $\mathbb R$. This allows us to take the limit inside and we get

$$\lim_{x \to 0} \sum_{k=1}^\infty \frac{(-1)^k}{(2k+1)!} x^{2k} = \sum_{k=1}^\infty \frac{(-1)^k}{(2k+1)!} 0^{2k} = 0$$

Answer 26

This is not a rigorous proof, but is instead an intuitive argument. Consider the graph of the sine function and in particular consider the origin $(0,0)$ and some arbitrary point $(x,\sin(x))$ a little bit to the right of it. Connect a secant line between the two points like so: Now consider the average rate of change of the sine function on that interval $[0,x]$, or alternatively the slope $m$ of that secant line, namely: $$m(x)=\frac{\sin(x)-\sin(0)}{x-0}$$ But clearly this is just $$m(x)=\frac{\sin(x)}{x}$$ But then "clearly" (again, this is just for intuitive purposes), as $x\to{0}$, the slope of this secant line approaches the slope of the tangent line to the graph at $x=0$ (i.e. it approaches whatever $\sin'(0)$ should be). Looking at the graph then, it shouldn't feel too unreasonable that this limiting procedure results in a $45$-degree diagonal tangent, hence a slope of $1$.

Answer 27

Here is a slick trick using elementary integration methods. Note that \begin{align} \int_0^1 \ \cos(xt) \ dt & = \left[ \dfrac{1}{x} \cdot\sin(xt) \right]_0^1 \\ & =\dfrac{\sin (x)}{x} - \dfrac{\sin (0)}{x} \\ & = \dfrac{\sin (x)}{x}. \end{align} Hence, \begin{align} \lim_{x \rightarrow 0} \dfrac{\sin (x)}{x} & = \lim_{x \rightarrow 0} \int _0^1 \ \cos(xt) \ dt \\ & = \int_0^1 \cos (0) \ dt \\ & =1. \end{align}