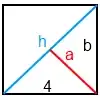
This is an extended addendum to all the neat proofs listed in the other answers to the post (and prompted by a reference request from @fish.frog):
There is no free lunch: All the proofs which use the notion of area (unlike the one via similarities) depend on the following
Theorem. There exists a function $A$ (usually called "area") on the set of all planar polygonal regions which takes values in ${\mathbb R}_+$, and which satisfies the following properties:
The function is invariant under congruences, that is, if $P, Q$ are congruent polygonal regions then $A(P)=A(Q)$.
The function $A$ is additive in the sense that if we subdivide a polygonal region $P$ in finitely many non-overlapping polygonal regions $P_1,...,P_n$ then
$$
A(P)=\sum_{i=1}^n A(P_i).
$$
If $P$ is a rectangle with the base $a$ and height $b$, then $A(P)=ab$.
Edit: the following is not needed, it follows from 1, 2 and 3 as noted by Hagen von Eitzen: $A(kP)=k^2A(P)$ where $kP$ is the dilation if $P$ by $k$.
Furthermore, if one has a well-developed notion of a limit (which Euclid did not have) then 3 can be replaced by a single normalization condition:
3'. $A(Q)=1$, where $Q$ is a unit square.
Existence of such function is not at all obvious (to a mathematician; anybody else would say that it is completely obvious, but this site is dedicated to mathematics). The shortest proof I know (using only axioms of Euclidean geometry) can be found in the book
E. Moise, "Elementary Geometry from an Advanced Standpoint" (3rd Edition).
The proof is long (about 10 pages) and rather tedious. (Somebody has to pay for a free lunch!)
Edit.: Proofs of existence of the area function for planar polygonal regions that one might see in a typical textbook or a class go as follows:
a. Compute area of triangle from the area of rectangles (Property 3). No attempt is made to show that different way to do so result in the same value of area of triangles.
b. Triangulate a polygonal region $P$ (in the convex case). No attempt is made to do this in the nonconvex case. (That's OK if one reduces attention only to convex polygons.) Proof of existence of a triangulation in the nonconvex case requires few clever but not difficult ideas. Archimedes could have done it (and maybe did!).
c. End of the story: No attempt is made to show that the result is independent of a triangulation, i.e., that the constructed area function is well-defined.
(This is not meant as a criticism of the common treatments of the notion of area, since there is only so much time and space one can devote to this topic, but to show where the problems arise and why a rigorous treatment is needed.)
Moise does a very thorough job here. His proof of c is very modern, it depends in the set of ideas used to prove "Schoenflies theorem" for simple closed polygonal curves in the plane: that every such curve bounds a planar polygon (that's Jordan's separation theorem in this context) which is homeomorphic to a convex polygon via a piecewise-linear homeomorphism. (Moise was a topologist.) I do not believe anybody could have done a proof that area is well-defined rigorously before, say, middle of the 19th century (Riemann integration or, alternatively, appearance of topology as a field).
By the way, Moise also gives several proofs of Pythagorean formula: Two using areas and one using similarities.
There are alternative ways to prove the theorem on existence of the area function, but, from what I know, they all require introduction of Cartesian coordinates on the Euclidean plane, which, in turn, depend on the Pythagorean formula. (One such approach is via Riemann or Lebesgue integration, developing which takes much more than 10 pages; another proof uses determinants.)

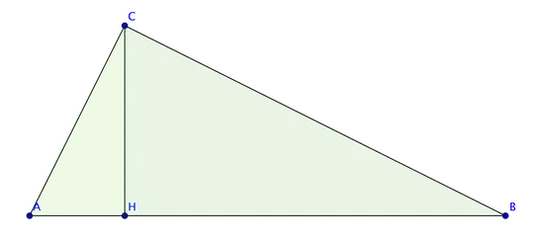

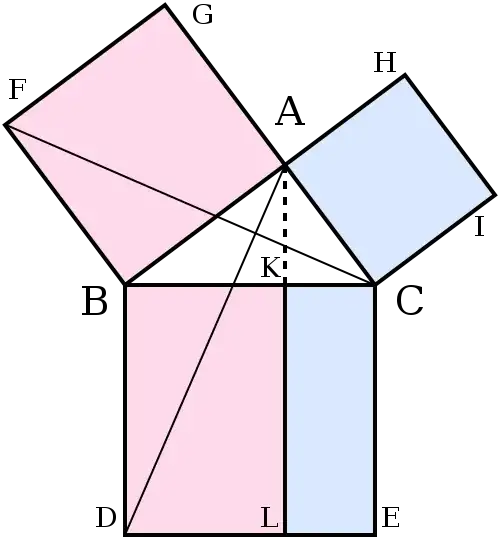



 Emanuele Paolini's thoughts about how any shape will do, not just a square, and that way of dividing a triangle he shows, and which robjon elaborates - those seem the likely routes to me. More thoughts
Emanuele Paolini's thoughts about how any shape will do, not just a square, and that way of dividing a triangle he shows, and which robjon elaborates - those seem the likely routes to me. More thoughts