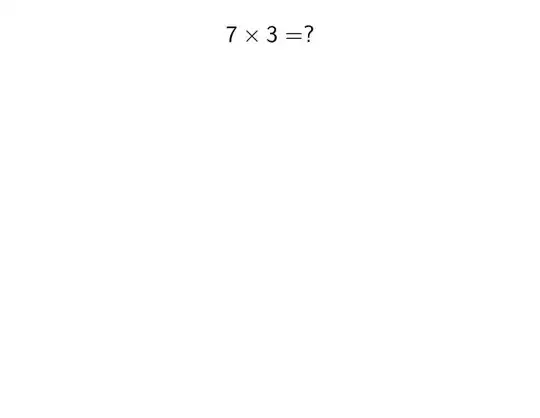110

With division, you can have a remainder (such as $5/2=2$ remainder $1$). Now my six year old son has asked me "Why is there no remainder with multiplication"? The obvious answer is "because it wouldn't make sense" or just "because". Somewhat I have the feeling that prime numbers are a bit like the remainders as you can never reach them with multiplication.

Is there a good answer to the question? (Other than the trivial ones?)

Additional comments after many answers are written:

I am really grateful for all the answers! It's a shame that I can't accept more than one. (A side note: I really hesitated to ask this question as I felt that this is a dumb question, I almost deleted it after I posted it. Now that I have received so many interesting points of view, I will try hard to find good examples when the next topic comes along to make him get a mathematical sense.)

What I lacked (or the math teacher/book) is answers like you gave before multiplication and division were introduced (as written in a comment).

Division with remainder is part of his math book (2nd grade, but a bit optional). So asking this question didn't surprise me that much.

I believe when he was taught the integer numbers, all examples (from me and perhaps the teacher) in the beginning were like "4 apples plus 5 apples equals ...". Then the math book introduces subtraction (still explainable with apples). With multiplication and division, the problems lost concrete examples and the "pure math" gets more dominant. And perhaps there was a bit too much focus on symmetry (plus and minus and multiply and divide are opposite), which is true, but not (obviously, that's where the question arose) completely true.

topskip
  • 1,111
  • 2
  • 8
  • 11
  • 2
    Thank you all for your very interesting answers! All with different approaches to the problem, and I will use them in my explanations. – topskip Sep 28 '13 at 15:26
  • 16
    What if you just ask him, "why would there be a remainder when you multiply?" And let him try to answer that. And emphasize word problems -- like instead of saying what's $27 \div 5$, say something like: if you have $27$ dollars and a pizza costs $5$ dollars, how many pizzas can you buy and how much money is left over. His question makes me want to double check that everything is clear to him in the context of word problems, without using terms like "remainder". – littleO Sep 28 '13 at 15:43
  • 3
    Because multiplication of natural numbers can be defined as repeated addition. – user5402 Sep 28 '13 at 19:53
  • You should explain what exactly is the operation of multiplication and division! Take a look at my answer below. Also, explaining him in some vague terms will confuse him more. – Mohan Sep 29 '13 at 03:52
  • I remember way back when I first learned about decimals, wondering why we even bothered with fractions. Knowing `5 / 2 = 2.5` and `2.5 * 2 = 5` meant this question just never occurred to me - they "exist" for both multiplication and division, but just have a special name sometimes. (A'course, now I know how useful fractions are, but sometimes I think we could be taught better) – Izkata Sep 30 '13 at 16:11
  • @Izkata Now I try to explain to a 2nd grader what $10/3$ is or $10/8$. I won't succeed. – topskip Sep 30 '13 at 16:40
  • Your kid is going to be a genius. A true mathematician. I don't think I even knew what a division was at the age of six. – Martijn Courteaux Sep 30 '13 at 21:20
  • @MartijnCourteaux As I wrote in the question (additional comments): division is in the math book he's doing (he has to do), so knowing division (and remainder) is expected. Perhaps he's going to be a mathematician? Or he's fed up with all the numbers and will do some serious work :) – topskip Sep 30 '13 at 22:28
  • 1
    @topskip: I disagree with "With multiplication and division, the problems lost concrete examples"—multiplication is "how many apples will you have if grandma gives you 5 apples every time you visit her, and you visit her 4 times" (20); division is easy to construct as well: "grandma has 27 apples; she promised to give you exactly 4 every time you visit her; how many times can you visit her before she can't give you exactly 4 apples any more and how many will she be left with?" (6 and 3); remove the "exactly" and "left with", and you can get him to think about fractions. – Erik Kaplun Oct 05 '13 at 08:27
  • @ErikAllik you are right, I used the wrong words in my "answer". What I meant is: the teaching in the beginning in _this_ class was about apples and now it's more just the math, only very few concrete examples. In general I totally agree with you (also as the answers have shown) that division and multiplication can be nicely illustrated by examples. – topskip Oct 05 '13 at 09:03

22 Answers22

88

Division does not have a remainder. The remainder is an artifact (do not use this word on a six year old) of an incomplete division.

When we do long division, a remainder can take place at any stage of the division process. In fact, a remainder keeps it going from one step to the next.

When we divide 529 by 3, what do we do first? We note that 3 "goes into" 5 one time, and from this, there is a remainder of 2. If we didn't care about accuracy down to the unit, we could just stop right there. We could pad our partial quotient with enough zeros to make $100$, and then append the remaining digits $29$ to the remainder. And thus $529\div 3 = 100, R\ 229$. Surely enough, checking our result, if we multiply $3\times 100$ we get $300$, and if we add $229$ to it, we get $529$.

Of course we know that $529\div 3$ isn't $100$. This is just an approximation which is good to within $100$. The actual number is in fact $100$-something. It's not less than $100$, and it's not $200$ or more.

Now usually we do not do this. We don't stop division at the hundreds or tens to take a funny remainder. We usually stop division at the units, and take the remainder there.

This is because many objects that we work with in the real world cannot be divided beyond the unit. If we want to distribute 13 toys among 4 children, everyone gets three toys, and there is a toy left over. We don't want to divide that toy into four, because it will be destroyed. Thus, we use a form of inexact mathematical division which gives us a model for this real-world constraint: integer division with a remainder.

But non-unit remainders can be useful too. Suppose we are distributing a large number of toys at the wholesale level, and there are 24 toys in a box. Customers must get a whole box; we do not divide boxes. Boxes are only opened in the retail store to sell individual toys.

Now suppose I have $1272$ toys in my warehouse and $5$ stores approach me, all wanting to buy $300$ toys. I don't have $1500$ toys, so I decide to give the customers an equal number of toys based on what I have. Now $1272 \div 5$ gives us $254.4$, or $254\ R\ 2$. Great, each customer can have $254$ toys, with two toys left over I can keep. But wait, the toys are in boxes of $24$, so that can't work! I cannot ship $254$ toys, because that is 10 whole boxes, plus 14 toys from an open box. The calculation has to be done with boxes, not with toys. In fact I have 53 boxes of toys, and I can give the customers 10 boxes each, and have 3 boxes left over. So the remainder is $3\times 24 = 72$ toys. In other words, in a real and useful sense, the remainder of dividing $1272 \div 5$ can be $240$ with remainder of $72$, when we require the result to be a multiple of 24.

So, on to the question: could there be a remainder in multiplication? The answer is no. A remainder is a special way of expressing the error in a calculation, peculiar to inexact division. We do not have to use a remainder to express the error in an inexact division: we can simply express division error as the difference between the approximate quotient and the exact one. For instance $17\div 8$ doesn't have to be $2\ R\ 1$; it could just be $2$ with an error of $-1/8$, since the exact quotient is $2\frac{1}{8}$ and $2 - 2\frac{1}{8} = -\frac{1}{8}$. The result is $\frac{1}{8}$ less than the exact result, and so that is the error.

Multiplications cannot have a remainder for two reasons. Firstly, multiplicationsare usually carried to completion and therefore exact. There is no reason why a multiplication of two integers would be left incomplete, in the same way that we can stop a division short and take stock of what is left. Secondly, multiplications can be inexact, when the inputs are fractions (possibly themselves inexact) and we truncate the result to a given number of significant digits. However, when multiplication is inexact, we do not express the error as a remainder.

The concept of "remaining" is peculiar to division. When we divide a number, and make the result slightly smaller so that the division "works out evenly" we have something "left over". This does not apply in multiplication.

Note also that in (ordinary) multiplication, the two operands are equivalent and it is commutative. In $5\times 4$ both values are products, and it is the same as $4\times 5$. One of the products is called a multiplicand and the other a multiplier, but they can readily switch roles. But in division $5\div 4$ is not $4\div 5$: dividend and divisor cannot switch roles, and the remainder is closely related to the divisor. So right off the bat we have a conceptual problem with a remainder in multiplication: which of the two products should be related to the remainder, like the divisor is in division? If we round off the result of a multiplication to some multiple, and choose to express the error as a remainder related to one of the products, should we choose the multiplicand? or the multiplier? And why?

Kaz
  • 6,671
  • 1
  • 17
  • 30
  • 8
    That is a great answer. Maybe still a little hard for six years but by the closest thing to a convincing explanation among the answers up to now. – Dirk Sep 28 '13 at 18:45
  • 1
    Along the lines of this answer, with long division you could also add a decimal and keep adding zeros to the dividend until you get tired of writing, or end with an exact result. This has the added value of easy demonstration with a calculator. – opello Sep 28 '13 at 19:03
  • 1
    Just signed up here in order to be able to upvote this answer. With regard on being hard for a 6 year old kid: my guess is that he may be having fractions in his mind already. In that case, the explanation that (the teacher?) introduced one particular way of division which has the additional rule to the game that fractions are not allowed. – cbeleites unhappy with SX Sep 29 '13 at 10:25
  • 3
    +1 but there is no reason to avoid using artifact(or any word for that matter) on a six year old, especially one that is asking questions like this one. – Mr.Mindor Sep 30 '13 at 15:09
  • 4
    "There is no reason why a multiplication of two integers would be left incomplete" - what if you don't need the full precision of the answer? This happens routinely when multiplying floating point binary numbers. The mantissas are multiplied as if they were integers, and the result is truncated. It's also commonly used when doing back-of-the-envelope style approximations. 325 x 135 is about 40,000 :) – Kuba hasn't forgotten Monica Oct 01 '13 at 11:09
81

I'd say it as "multiplication is always exact - when you multiply two and three, the answer is exactly six."

When you divide, you are essentially doing the opposite of multiplication, and division is not exact. If you are dividing seven by $2$, you get a result of $3$ with a remainder of 1 because 3 times $2$ is "as close as possible" to $7$ as you can get without going over, but you still have an error, $1$.

You can say also, "When you get to fractions, you won't need a remainder, you get one result."

Another question is, why don't you get a remainder when you subtract? There is actually a time when you can get an error when you subtract - when dealing with non-negative numbers. For example, what is $3-6$ if you only know $0,1,2,\dots$? In that case, you could say the result is $0$ with an error of $3$. But when we learn about negative numbers, we say instead that the result is $-3$.

Thomas Andrews
  • 164,948
  • 17
  • 196
  • 376
  • 4
    I think both multiplication and division are exact because mathematics is exact. :-) – kiss my armpit Sep 29 '13 at 16:05
  • 13
    But that's just pedantry, @PGFTricks. We often talk about estimation and errors. We use the term "exact" often in mathematics, when talking about estimations and the like. When talking with a six year old, what do you think "18 divided by 6 is 3, exactly," means? – Thomas Andrews Sep 29 '13 at 16:09
62

Sounds like a smart kid - they always come up with interesting questions! I'd approach it something like this.

Division lets you answer questions like, "If a box holds four apples and I have thirteen apples, how many boxes can I fill?" The answer is $13\div 4=3$, with remainder $1$. That means that you'll fill three boxes and have one apple left over, which is what "remainder" means.

Multiplication lets you answer questions like, "I have three boxes, each containing four apples. How many apples do I have?" This time, the answer is $3\times 4=12$. There's no remainder because there's nothing left over because all the apples were in full boxes to start with.

David Richerby
  • 2,420
  • 1
  • 16
  • 24
  • 4
    I'd say: "... were in **completely filled** boxes to start with." - that will quite naturally solve the intersting problem how those other numbers (such as 13) could be obtained by multiplication, that "cannot" be divided by 4. – cbeleites unhappy with SX Sep 29 '13 at 10:19
59

I'll try it the 'Lego way' (sorry for the publicity)

When we multiply two positive numbers we get 'perfect' rectangles ($48=6\times 8$) :

$\qquad$ lego

When we add some small squares at the bottom of the rectangle and divide by the width we get a remainder except if we added the whole width again ($52=6\times 8+4$) :

$\qquad$ remainder

Raymond Manzoni
  • 41,072
  • 5
  • 79
  • 133
  • 2
    Nice! I think this answer suits the OP's request the best. – dreamer Sep 29 '13 at 08:56
  • 4
    Legos are also a nice manipulative for introducing fractions. An example NCTM article: http://faculty.tamucc.edu/sives/1350/tcm2011-04-498a.pdf – Benjamin Dickman Sep 29 '13 at 18:31
  • 3
    You're looking for http://bricks.stackexchange.com/ – Christian Chapman Sep 30 '13 at 23:07
  • 10
    Maybe it's just me, but I did not get the explanation. – Sunny R Gupta Oct 01 '13 at 06:37
  • 2
    (late details...) To divide a positive number $N$ by $6$ add as many lines of $6$ squares as possible to get a total of $N$ squares. In the first picture we could add $8$ lines (the quotient) to get $N=48$ with no remainder. In the second picture $N=52$ so that we could add $8$ lines too but with a remainder of $4$. This should make clear that we will get a non zero remainder except for $N$ an exact multiple of $6$. – Raymond Manzoni Mar 31 '14 at 11:54
34

What a charming question, and very interesting answers.

I would say simply that multiplication is a fast way of adding; when you add things, there's no quantity that is left over. Division is a fast way of subtracting, and the whole point of subtraction is to find out what is left over when something is taken away.

Eric Lippert
  • 3,428
  • 1
  • 18
  • 18
  • 1
    Nice to see you posting on math.stackexchange, I liked your [hotel room key analogy](http://stackoverflow.com/questions/6441218/can-a-local-variables-memory-be-accessed-outside-its-scope) for pointers on stackoverflow. – littleO Sep 29 '13 at 05:43
  • The whole point of * is to discover a single number. The whole point of division is to discover a single number. Wait, why does multiplication produces one number, as required, but division gives you two: the quotient and reminder? – Val Sep 29 '13 at 17:53
  • @Val division does only give you one number, if you don't get lazy and stop before you get to it. (As noted above in the answer by @Kaz.) – Hellion Sep 30 '13 at 20:29
  • @Hellion Use the hiperlinking. I do not see neither Kaz nor anybody else who can say that quotient is not a result of division. – Val Sep 30 '13 at 21:13
  • @Hellion, or if you *can* get to it, e.g. 1/3 – Wayne Werner Sep 30 '13 at 21:14
24

I think that kids who ask such smart questions often do not need answers but more questions. In this case I would reply: Why do you think that there could be a remainder? What should a remainder for multiplication be? Should there also be a remainder for addition? And for subtraction?

Here it is getting most interesting! If he can already add, subtract, multiply and knows what division is, he probably already knows negative numbers. If not, he may be able to grasp the idea easily. In fact, there is a "remainder" for subtraction! What is 8-10? It's 0 with a remainder of 2! Now you could talk about the similarity here. Subtraction undoes addition as division undoes multiplication. In both cases, sometimes the undoing works, sometimes not perfectly. For subtraction you "invent" or "define" new numbers, the negative numbers, and then the remainder is gone. When he got this idea, you could also try to go ahead and try to "invent" the numbers which are needed to make division work. If he got this, wait until he knows about exponentiation and roots...

Dirk
  • 11,270
  • 34
  • 57
  • 2
    I think this is exactly the cause of the question (symmetry): plus and minus, multiply and divide. _I_ was thinking of something like this: we can get to all number by dividing something by something else, but we cannot get to all numbers by multiplying something by something else (prime numbers). So the remainder could be: If I want to get to 7, I multiply 2 by 3 and add the remainder 1. While this makes no sense in the mathematical world, it _could_ be one part of the symmetry (not really serious with the answer, just an idea) – topskip Sep 28 '13 at 19:23
  • From a pedagogical point of view, this is the best answer for "what should I tell the questioner?". Always answer a question with another question, so the questioner forms their own answer. Then he will someday provide *us* with the right answer! – levitopher Sep 29 '13 at 05:33
  • I like the "remainder" concept for subtraction, especially since there are some real-world situations where things can't go negative, but can be "left over". There's a pile of 12 objects and a box which holds 15 and has space for 9 more. One can't put all the objects into the box so as to have space for -1 more, but one can put 9 more objects into the box (bringing its total up to 24) leaving 3 in the pile. – supercat Mar 04 '14 at 20:17
23

The answer is that the integers (or natural numbers) are a ring. That is, you can add, subtract, and multiply, but not necessarily divide. Other examples of rings are matrices and modular arithmetic.

If you instead dealt with fractions, that would be a field, where indeed you could always divide with no remainder. (except by 0).

In terms of explaining to your 6yo, probably your best bet is to say that "division is the hardest operation, so sometimes you get a remainder".

vadim123
  • 81,238
  • 9
  • 112
  • 215
  • 1
    Thanks. I will re-read about rings and such and try to find a very simple answer... – topskip Sep 28 '13 at 15:13
  • 36
    The first part does not seem helpful for a six year old and the last part does not carry any explanation. – Dirk Sep 28 '13 at 18:40
  • 15
    @topskip This explanation is totally unhelpful for the question you've asked; I suggest you "unaccept" it and read through some of the others. Discussing *rings* and *fields* is not a good way to broach such a question with a six year old, nor is the dismissive final sentence. – Benjamin Dickman Sep 28 '13 at 18:51
  • 3
    Well, integers (not natural numbers) form a ring because of the properties they have not the others way. – user5402 Sep 28 '13 at 19:52
  • 6
    @BenjaminDickman thanks. Now that there are so may very well written answers, I will read them all in depth and accept the one that helps _me_ most explaining it. – topskip Sep 29 '13 at 06:30
  • 10
    "Daddy, I heard that differential equations are even harder than division. Do they have remainders, too?" – David Richerby Sep 30 '13 at 11:36
  • 3
    I have been explaining what a ring is to my 8 year old, and she took it in without complaint. It's not a very hard concept unless one has some bad memories from college :) – Kuba hasn't forgotten Monica Oct 01 '13 at 11:11
17

Animation can help your son understand it better.

Division

enter image description here

Multiplication

enter image description here

kiss my armpit
  • 3,690
  • 5
  • 23
  • 38
  • I wanted to do it myself but failed to explain why there is reminder division but not in multiplication. – Val Sep 29 '13 at 08:42
  • 1
    @Val: OK. Then explain to the students that this problem is similar to "why can't $\textrm{d}x$ be a denominator as in $\int \frac{f(x)}{\textrm{d}x}$? or why can't a vector be a denominator as in $\frac{\vec{A}}{\vec{B}}$?" – kiss my armpit Sep 29 '13 at 08:45
  • That is an interesting question. I guess that you should accumulate infinitecimals under integration. You get infinitesimals when dx is a factor reather than divisor. When dx is a divisor you will have continuum of infinities to integrate, which is infinity obviously. But I do not understand how is this clarifies the reminder issue. – Val Sep 29 '13 at 09:00
9

Multiplication is what you do when you know some facts in advance and want an answer which leaves no remainder. At an elementary level, how many cakes or pizza slices do I need so I can share them round with none left over?

A remainder is what I get when I didn't plan ahead, or someone doesn't turn up, or there are two extra people, or I had to guess how much I would need, or someone drops a pizza on the floor and throws it away.

These very physical ways of dealing with multiplication, though, are only illustrations - they give an intuition as to why remainders might make sense etc - but they don't adequately fit all the situations in which the concept gets used, and sometimes people who have been taught numbers in a very physical way get stuck when new concepts arise. As I was roughly told by someone I know: "I could never understand negative numbers, because we were taught to count bananas, and I never could get my head around a negative banana."

Mark Bennet
  • 96,480
  • 12
  • 109
  • 215
  • 2
    IMHO, "half a banana" is a very natural concept, which poses no difficulties at all to a very physical interpretation. In fact my concept of division as a child would rather insist that the restriction not to divide the usual "units" (cakes, pieces of cake, apples, bananas, houses) into smaller parts is an artificial rule that doesn't line up well with the physical world. If you want to explain integer division, why not distribute 4 "real" dogs among 3 children - or other "units" where the restriction not to allow further division of the unit is more sensible? – cbeleites unhappy with SX Sep 29 '13 at 11:31
5

There is a "remainder" in multiplication. It is called "carry". The difference is that you can put the "carry" from multiplication back into the final result, while you can't put the division remainder into the final result.

9/5 is 1 with 4 remainder, which you write as "1 r 5" (as I was taught),

9*5 is 5 with 4 carry, but you can put the carry into the answer by writing "45"

This not quite the correct answer and mathematicians will cringe (the carry is a result of partial result in base 10 long arithmetic, the division remainder (modulo) has nothing to do with choice of base), but it should satisfy the 6 year old.

Mark Lakata
  • 1,090
  • 6
  • 7
5

Maybe it would be good to find out why he asks this question:

  • because he's genuinely interested in why a new concept of "remainder" pops up, as opposed to
  • because he thinks the concept of remainder is just silly: everyone knows how to divide 1 apple into 4, well, quarters.

I say that because I remember that when I was told in school that "you cannot divide 3 by 4" (leading up to the remainder) I thought the teacher was telling us complete crap.
Some 20 years later, I met someone doing research about maths teaching, and she told us that the concept of fractions is one of particular difficulty in teaching maths. She said, there are kids who have that concept naturally, and others that just never get their head around. She further thought it unlikely that anyone in the audience (natural scientists, mathematicians, computer scientists and engineers) would even be able to imagine how it is without this concept, which I guess applies to maths.SE as well. I guess a 6yo who is firm in multiplication (at the beginning of probably his 1st year in school) belongs to the first group.

I'd tell him that there are different types of division, which are useful for answering different questions or describing different situations.

Imagine that there a 4 pieces of cake, and 3 people. Now, in the first round *, everyone can have 1 piece. One piece is left over. What to do with that?

  • Put remainder into the fridge: school version of integer division. Noone cares what happens to the remainder.
  • Divide the remaining piece of cake into 3 thirds, and give everyone $\frac{1}{3}$ piece of cake. (Division with fractions, problem of leftovers solved)

  • Daddy gets a second piece of cake. Problem with leftovers solved, but integer division again.
    (Though, if you tell the idea with daddy getting the additional piece of cake, he may take to dislike integer division. Maybe it would be better to tell the idea with son getting the additional piece...)

  • But while the restriction not to cut the piece of cake into smaller pieces seems somewhat arbitrary (and particularly so if daddy is the only one to get more cake ;-) ) the remainder-type of division is genuinely useful for some situations: "There are 13 apples. They are put into boxes that hold 6 apples each. How many full boxes do we get?" as there are sensible situations where only full boxes are useful.

  • You can also talk with him about the differences between things like cakes and apples that can sensbily be divided further, and other things that can not (such as live dogs). Although even there are interpretations of fractions that apply: if someone owns half a house, the house is shared with someone else. You could have half a dog the same way.
    Do not forget this one Sendung mit der Maus: Blinker

* if you like, you can start here to smooth the ground for the invention of the algorithm of written out division as in @Kaz's answer (though I guess the 6yo in Germany will have to wait patiently some more years until school finally arrives there)

cbeleites unhappy with SX
  • 151
  • 4
  • Your suggested questions on probing what the child is thinking are excellent. Your second paragraph about what the education researcher said reminds me very much of my grandmother, and how bewildered both I and she made each other when I was asserting (I think I was about 8 years old) that the numbers were a continuous line (actually, I thought of them as a coiled-up, self similar helix so that scaling by 10 doesn't change the picture) and that fractions were simply about zooming in on the line. She was dumbfounded by the idea and spoke of her longstanding difficulty with fractions - ..... – Selene Routley Oct 17 '17 at 23:22
  • .... we seemed to be fundamentally different. I think I was a bit slow on the uptake in these matters; it took me a long time to understand that people have different ways of thinking about mathematical concepts. Roger Penrose also has some interesting tales about discussions of fractions in his class in the first chapter of "Road to Reality" that I and probably you could relate to. – Selene Routley Oct 17 '17 at 23:24
  • +1 Wish I could upvote this twice. – user0 Aug 24 '18 at 13:57
4

Your son is very perceptive! I think a possible answer is that "multiplication with remainder" hasn't been invented (or discovered?) yet. Ask him what "2 times 2 with remainder 1" should be. Can he devise a ternary operation (one with three inputs) that reverses the effect of division?

Bob Pego
  • 4,999
  • 3
  • 24
  • 18
  • 1
    Interesting thought! Thanks – topskip Sep 28 '13 at 16:06
  • 2
    One can proove that any number can be written as a product of two numbers, plus a remainder. – Kile Damgaard Asmussen Sep 28 '13 at 19:14
  • I think "two times two with remainder 1" should be $2\times2+1=4+1=5$ – Kartik Sep 29 '13 at 15:31
  • 2
    @Kartik now you just have to explain why 2 * (7/3) = 5. – Alistair Buxton Sep 29 '13 at 20:32
  • @KarlDamgaardAsmussen : Of course, n = 1*1 + (n-1). But I guess that's not what you meant. I think you're looking for multiplication _modulo m_, which does have a result that looks like a remainder. E.g. 2 x 12 (_modulo 10_) = 4. Using modulo 10 is easy if you're used to decimal. And you can explain it with boxes of apples which you repack: 2 boxes of 12 apples, and new boxes which can hold 10 apples each. – MSalters Sep 30 '13 at 21:08
  • @MSalters I should perhaps have specified so, curse the imprecise english language! I meant modulo arithmetic, yes. – Kile Damgaard Asmussen Oct 16 '13 at 00:13
  • $$2\times \frac{7}{3} = 5$$ $$2 = \frac{5}{7/3} = \frac{3\times 5}{7} = \frac{15}{7} = 7\times 2 + 1 ?$$ Wait.... was that supposed to be taken seriously...? – Mr Pie Oct 02 '17 at 07:34
3

He noticed that modulus is attached to integer division operator /, so he's asking what else it is attached to.

I would tell him that there are 5 basic operations now: +, -, *, / and modulus. Division helps calculate modulus.

Multiplication also helps calculate modulus:

5 / 2 = 2

5 - 2 * 2 = 1

So does subtraction:

5 / 2 = 2

5 - 2 - 2 = 1

So does addition:

5 / 2 = 2

5 - (2 + 2) = 1

I think he's just trying to place the missing information about the new operation.

pwned
  • 437
  • 4
  • 10
2

For the purposes of six year old math:

Division is about taking steps backwards towards $0$, and, in particular, taking as many as you can without overstepping. If you get to a number from which the next step would go past $0$, stop on that number: this is your remainder.

Multiplication is about taking steps forwards. There is no target in mind, like there is with the $0$ in division, so the only question is where you stop after you've taken your steps.

As far as your hunch about primes: One way to explain this, in the context of six year old multiplication, is that the only way your forward steps can end up on a prime $p$ is if either you just took your one and only step (and it was a step of size $p$) or you just took a total of $p$ steps (each of size $1$).

You could now consider what it means to step your way to a composite number, but I'll end my post here by remarking that it's quite impressive for a six year old to grasp the concepts of multiplication, division, and (perhaps) being prime!

Benjamin Dickman
  • 13,259
  • 2
  • 39
  • 82
  • Well, he's really not bad in math, but division and remainder is in his schoolbook (2nd grade), so its within the expected curriculum. – topskip Sep 28 '13 at 19:27
  • 1
    @topskip Interesting. One other point: You may wish to look at how he has learned about multiplication and division, so that (if appropriate) you can similar language in answering his questions. My answer above is designed for kids who have been learning about multiplication and division by moving along number lines (in "steps") but you might ask *him* to try and answer the question, and then use his terminology in crafting a response. – Benjamin Dickman Sep 29 '13 at 18:41
1

Since he is 6 years old probably he only knows about natural numbers. So explain that when we multiply we are adding a number with itself and so there is no remainder because we are increasing the sum.

Sigur
  • 6,028
  • 2
  • 24
  • 44
  • 1
    I'd expect a 6yo to be perfectly fine with fractions like quarter of an apple, a third of a cake, half an hour. The only place where he's not supposed to know this is probably at his maths class in school... – cbeleites unhappy with SX Sep 29 '13 at 11:53
1

The reason why this is is that division is the undoing of multiplication. Multiplication is designed so that it always has an answer, but division (particularly for integers) it is just finding what you must multiply to get some number. Sometimes this number does not exist, and so we must get close. Remainders tell us how close we are, particularly, what we must add to get to the right answer.

PyRulez
  • 9,530
  • 3
  • 34
  • 98
1

The correct answer to this question is that because the concept of remainder doesn't make any sense in case of multiplication. So, you have to basically explain him, what remainder is!

Multiplication is nothing but repeated addition. When you multiply two numbers m.n , you are basically adding m n times. As you don't have any remainder while adding numbers, there shouldn't be remainder while multiply numbers too!

But division is a very different operation, when you divide a natural number n by m. You are basiically trying to write n as sum of finite numbers of m. But unfortunately, you can't always do that. You can't write every natural number as the repeated sum of another natural number. For example, you can't write 11 as repeated sum of 2.Why? Because 2+2+2+2+2 is less than 11 but 2+2+2+2+2+2 is greater than 11! So, we have proved 11 can't be written as sum of 2s.But we can try our best. We can write 11 as 2+2+2+2+2+1, that we can write 11 as sum of 2s plus one smaller number than 2 that is one. Now this smaller number is called the remainder!

Mohan
  • 13,820
  • 17
  • 72
  • 125
1

Suppose you have a pie. There are no leftovers (remainders) because the pie is uncut, and in one piece. You can only speak of leftovers when you know in how many pieces you will cut the pie, and how many people want a piece of pie.

When you cut the pie in 4, and 3 people want a piece, there will be one leftover.

If you decide to bake 10 more pies, there are no leftovers until you start to cut (devide) them, and ask asked the people how many want a piece.

het.oosten
  • 111
  • 1
1

Division is just repeated subtraction ie how many times do I take 4 away from 12 to get 0 is identical to 12/4.

Sometimes when you take a number away from another it does not get to 0 you end up with a bit left over.

When you multiply you are not aiming at a specific number (in division's case 0) so there is no remainder, you just arrive exactly at wherever the numbers send you.

Stefan
  • 111
  • 3
1

With division, sometimes there can be a remainder in the answer:

You are putting apples into boxes. You have 13 apples. Each box holds 4 apples. How many boxes do you need?

With multiplication, sometimes there can be a remainder in the question:

You have 3 boxes of apples, plus one apple that is not in a box. Each box holds 4 apples. How many apples do you have?

mob
  • 111
  • 3
0

When you multiply a whole number, say $6$, by another whole number the result is constrained to be one of $6, 12, 18 ,24, \ldots$. So if you want to think of division as an inverse to multiplication, this interpretation only makes sense (with respect to $6$) if you divide one of $6, 12, 18 ,24, \ldots$ by $6$. Thus when thinking of division as an inverse operation, it should always be thought of as an inverse with respect to some other number (which in my example was $6$), then as in multiplication there is no remainder.

dezign
  • 1,577
  • 9
  • 11
0

Division has a remainder in the case that we "disregard" the fractional component of the quotient.

For example:

10/4 = 2 remainder 2
10/4 = 2.5

The decimal component of the true expression corresponds to the remainder in first expression. That is, we have 0.5 4's left over, 2.

The same can be seen if we "disregard" the fractional component when multiplying an integer by a rational number.

For example:

2.5 * 4 = 10
2.5 * 4 = (2 * 4) + (.5 * 4) = 8 + 2

This is often how I do multiplication in my head. I multiply from the left, successively adding the products.

That is:

24301 * 99 = (20000 * 90) + (20000 * 9) + (4000 * 90) + (4000 * 9) + (300 * 90) + (300 * 9) + (1 * 90) + (1 * 9)

The same can be done with rational numbers, and the portion with the fractional bit is the "remainder".

blaklaybul
  • 321
  • 1
  • 6