86

The series $$\sum_{n=1}^{\infty}\frac{1}{n(n+1)}=1$$ suggests it might be possible to tile a $1\times1$ square with nonrepeated rectangles of the form $\frac{1}{n}\times\frac{1}{n+1}$. Is there a known regular way to do this? Just playing and not having any specific algorithm, I got as far as the picture below, which serves more to get a feel for what I am looking for.

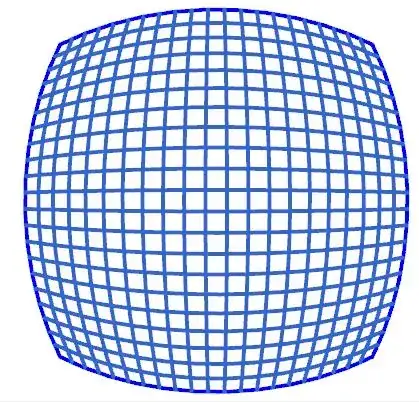
Tiling of Square with rectangles

I think some theory about Egyptian fractions would help. It's nice for instance in the center where $\frac13+\frac14+\frac16+\frac14=1$. And on the right edge where $\frac12+\frac13+\frac16=1$.

Side note: The series is $\left(\frac11-\frac12\right)+\left(\frac12-\frac13\right)+\left(\frac13-\frac14\right)+\cdots$. The similar looking $\left(\frac11-\frac12\right)+\left(\frac13-\frac14\right)+\left(\frac15-\frac16\right)+\cdots$ sums to $\ln(2)$, and there is a nice picture for that, if you interpret $\ln(2)$ as an area under $y= \frac{1}{x}$:

Tiling of ln(2) with rectangles

2'5 9'2
  • 51,425
  • 6
  • 76
  • 143
  • 3
    Wow! This is the most interesting question I've seen on this site in a while :) – Zubin Mukerjee Feb 24 '15 at 23:12
  • 14
    This is a research level problem in "Concrete Mathematics" (2nd edition) by Grapham, Knuth, Patashnik (ISBN-10: 0201558025): see page 66, exercise 37. In the section with hints you will find that every one of the authors has a different opinion. – Moritz Feb 24 '15 at 23:15
  • 13
    This was asked at MO: http://mathoverflow.net/questions/34145/can-we-cover-the-unit-square-by-these-rectangles and it appears to still be an open problem. – Samuel Feb 24 '15 at 23:20
  • 5
    I wrote a paper related to this (http://www.math.ubc.ca/~gerg/index.shtml?abstract=CTGP). Therein you can find a reference to this problem statement, as well as my reason for believing that such a packing is possible. – Greg Martin Feb 24 '15 at 23:40
  • What's protocol for when a question turns out to be research level? Should I delete the question? – 2'5 9'2 Feb 25 '15 at 00:31
  • @alex.jordan Generally, a question should not be deleted unless it is unsalvageably awful (e.g. do my homework for me), inappropriate, or spam. As it stands your question is none of these and does not deserve deletion at all. – nanofarad Feb 25 '15 at 01:56
  • @GregMartin: Do you happen to know of a non-trivial tiling (not geometric like golden ratio or similar), with no two equal tiles, which *does* have some kind of enumeration for each different tiling? – Alex R. Feb 25 '15 at 02:11
  • What is your algorithm for placing the rectangle in the picture where the area sums to $\ln 2$? – Greg Martin Feb 25 '15 at 02:30
  • 1
    @GregMartin I can't take credit for that; I saw it somewhere at some point. After the big rectangle for $1-\frac12$, the real pattern sets in. First, using $x=1+\frac12$, we get the rectangle representing $\frac13-\frac14$. Then at $x=1+\frac14$ and $x=1+\frac34$, you get the rectangles for $\frac15-\frac16$ and $\frac17-\frac18$. Then at $x=1+\frac18$, $x=1+\frac38$, $x=1+\frac58$, and $x=1+\frac78$, you get rectangles for $\frac19-\frac1{10}$, $\frac1{11}-\frac1{12}$, $\frac1{13}-\frac1{14}$, and $\frac1{15}-\frac1{16}$. Do you see the pattern? Look for powers of $2$ in denominators. – 2'5 9'2 Feb 25 '15 at 03:34
  • 2
    Since no one seems to know how to fit the rectangles into a square of area equal to the sum of their areas, how about this question: What is the smallest square that contains all the $\frac1{n}\times \frac1{n+1}$ rectangles with no overlaps? – marty cohen Feb 25 '15 at 04:02
  • @martycohen : look at either of the links in the above comments. Paulhus has fit them into a square of side length something like $1+10^{-9}$. – Greg Martin Feb 25 '15 at 17:32
  • 1
    @alex.jordan : Thanks for the explanation; it's a cool fact. I note that the $\ln2$ example tiles the curved area with rectangles of given area, but not with given dimensions in any reasonable way. The analogous problem would be to tile the unit square with rectangles of area $1/n(n+1)$ but not with given dimensions; and that's trivial. So I think we're still looking for an example of a natural known tiling with a sequence of rectangles of given dimensions. – Greg Martin Feb 25 '15 at 17:37
  • @GregMartin What is "not with given dimensions"? – VividD May 24 '15 at 08:17
  • @VividD He means that the rectangles from the $\ln(2)$ example are not literally $\frac{1}{2n-1}\times\frac{1}{2n}$. They have that same total area, but different dimensions. – 2'5 9'2 May 24 '15 at 16:24
  • @alex.jordan Oh, ok, now I see. – VividD May 24 '15 at 16:26
  • Nice problem. But there seems to be no method of arrangeing it analytically. – OKPALA MMADUABUCHI Jun 08 '15 at 22:43
  • I ❤ this question !!!!!!!!! – Spectre Oct 04 '20 at 08:22
  • And that's popularity.... – Spectre Oct 04 '20 at 08:22
  • This question is basically identical to one posted on [MathOverflow](https://mathoverflow.net/questions/34145/). I am leaving the question here as a reference for interested readers in the future. – Xander Henderson Dec 20 '20 at 18:18

0 Answers0